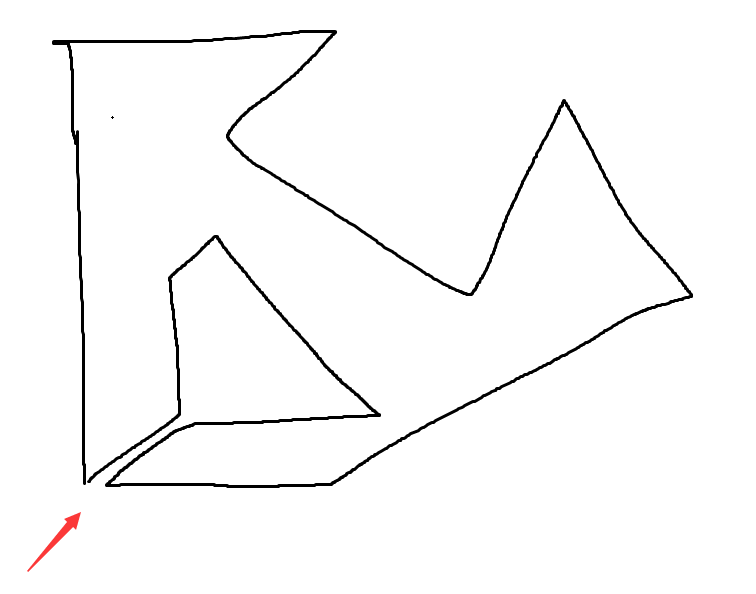README.md 20 KB
Recast Navmesh
推荐文章
- 知乎
Recast Navigation源码解析:https://zhuanlan.zhihu.com/p/484520809 - 知乎
Recast Navigation基础:https://zhuanlan.zhihu.com/p/74537236 Recast Tutorial:https://digestingduck.blogspot.com/2010/02/slides-from-past.html
重要论文
- Path Planning for a vision-based autonomous robot
- Simplified 3D Movement and Pathingfinding Using Navigation Meshes
- Volumetric cell-and-portal generation
- Crowdws In A Polygon Soup: Next-Gen Path Planning (GDC, 推荐)
导论
根据时间顺序,有这么几个重要概念被提出
| 里程碑 | 作者 | 时间 |
|---|---|---|
| Meadow Mapping | Ronald C. Arkin | 1986 |
| Volumetric Cell-and-protal generation | Denis Haumont | 2003 |
| Corwds In A Polygon Soup: Next-Gen Path Planning | David Miles | 2006 |
| Recast Navigation | Mikko Mononen | 2008 |
Meadow Mapping
Ronald C. Arkin 是一位美国计算机科学家,他在 1987 年发表了一篇论文 《Path planning for a vision-based autonomous robot》 ,介绍了 Meadow mapping 的原理和实现
Meadow mapping 是一种用于生成导航网格的方法,它将自由空间分解成凸多边形的集合,然后以每个凸多边形的边缘中点作为寻路节点,使用 A* 算法进行寻路。它还可以根据不同的地形类型(如人行道,草地,砾石等)设置不同的代价函数,优化寻路结果。它是现代 Navmesh 系统的雏形。
Path planning for a vision-based autonomous robot 论文)
Meadow Mapping 提出一个概念:把世界凸多边形化
为什么是凸多边形?
- 凸多边形内任意俩点连接不会超出多边形区域
- 凸多边形边上的点便于做寻路最小单位
凸多边形内部不需要寻路
我们只需要将世界划分成多个凸多边形,那么就只需要研究凸多边形之间如何连通即可,凸多边形内部直接一根直线连接即可
于是我们将寻路问题转换为以凸多边形边缘中心为节点的图论搜索问题
为什么不用 Grid (网格) ?
对于大面积的开放区域来说,格子作为寻路基本单位则数量庞大;但是一个凸多边形可以是一个很大的区域,所以对于寻路来凸多边形的效率更高
所以一个寻路流程大概如下
- 得到一个 3D 场景
- 获得可行走区域
Reachable Space(以前是手动绘制,现在可以自动绘制) - 将可行走区域划分成多个凸多边形
Convexify the Space - 凸多边形为单位,继续路径查询
Path Finding - 路径改进,得到更为平滑的路径
那么会有这么几个问题?
- 如何自动绘制可行走区域
- 如何区域划分凸多边形
- 如何进行路径查询
区域划分凸多边形
如果区域是凸多边形,则直接结束算法
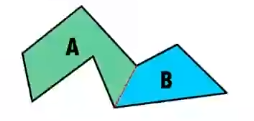
如果区域不是凸多边形,则找到一个凹的角(>180°),尝试将其与多边形内部其他的点连接起来,这个时候会得到两个新的区域,也就是上图的 A 和 B,然后对这两个区域再进行相同的算法,如此一来整个场景就都是凸多边形
也就是递归的二分法
- 如何判断一个多边形是凸多边形?
检查是否存在大于 180° 的角
规定凸多边形节点顺序按照逆时针走
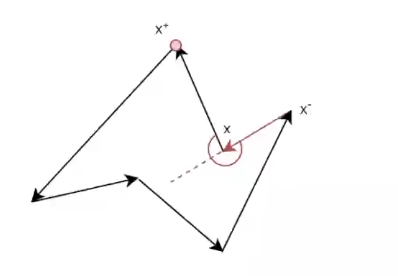
向量 (x-, x) 和向量 (x, x+) 进行叉乘,可以判断点 x+ 在向量 (x-, x) 的左边还是右边。叉乘的结果如果是正数那么就是在左边,反之在右边
以上图为例,点 x+ 在向量 (x-, x) 的右边,那么这个点的角度大于 180°
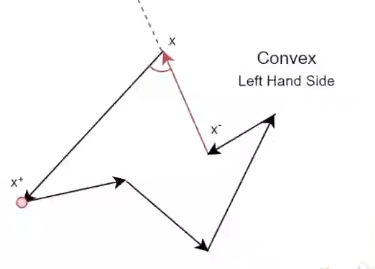
以上图为例,点 x+ 在向量 (x-, x) 的左边,那么这个点的角度小于180°
通过上面的发现,我们只需要遍历凸多边形所有的点,即可判断每个点的角度是否大于180°,以此判断该多边形是否是凸多边形
- 如何将大于 180° 角的点连接到多边形其他可见顶点上?
检查所有多边形节点与之连线是否为对角线
- 对角线的要求
- 条件1:不与多边形的边相交
- 条件2:在多边形内部
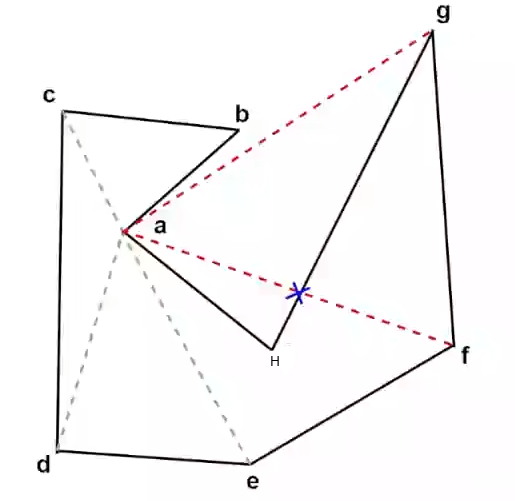
上图中 af 与 gh 相交,不符合条件1 上图中 ag 不在多边形内部,不符合条件2
以凹点 a 为例,对 a 点来说 g、f 两点就是不可见的,因为 ag 连线完全在多边形外,af 连线与 gh 连线相交
这里推荐一本书 《Computational Geometry in C》
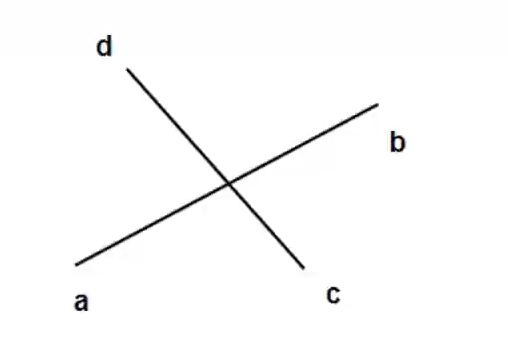
如何判断 af 和 gh 线段相交?
高中数学提供的解决方案就是点斜式求斜率,然后进行计算。但是在计算机中,直接根据 k = (y2 - y1) / (x2 - x1) 算出来使用 double 存储可能存在精度问题,或者除 0 错误
这里依然使用叉乘的思想
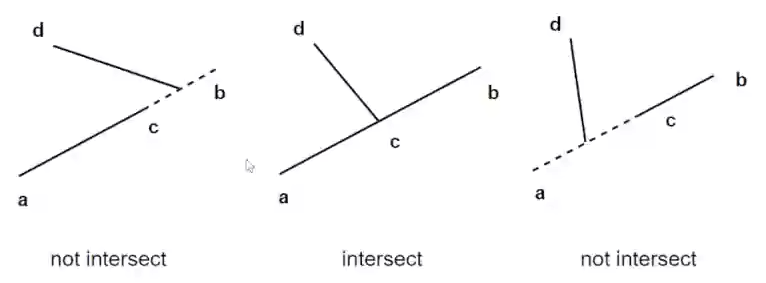
如果 a、b 两点在 dc 线段的两端,并且 d、c 两点在 ab 线段的两端,那么线段 ab 和 dc 相交
bool isCross(Vector2D a, Vector2D b, Vector2D c, Vector2D d) {
// c、d 两点在线段 ab 的两端
bool cd_cross = isLeft(a, b, c) ^ isLeft(a, b, d);
// a、b 两点在线段 cd 的两端
bool ab_cross = isLeft(c, d, a) ^ isLeft(c, d, b);
return cd_cross && ab_cross;
}
上述代码使用异或来判断是否满足两点在线段两端的判断,如果两点都在右边或者都在左边,那么异或的结果就是 false,如果两点一个在左边一个在右边则异或的结果是 true
但是上述解法无法处理共线问题,比如上图所示,点 c 在线段 ab 上,所以需要额外判断共线问题
所以判断线段是否相交的大概算法如下
bool isCross(Vector2D a, Vector2D b, Vector2D c, Vector2D d) {
if (c 与 ab 共线) {
return c 是否在线段 ab 上;
}
if (d 与 ab 共线) {
return d 是否在线段 ab 上;
}
if (a 与 cd 共线) {
return a 是否在线段 cd 上;
}
if (b 与 cd 共线) {
return b 是否在线段 cd 上;
}
// c、d 两点在线段 ab 的两端
bool cd_cross = isLeft(a, b, c) ^ isLeft(a, b, d);
// a、b 两点在线段 cd 的两端
bool ab_cross = isLeft(c, d, a) ^ isLeft(c, d, b);
return cd_cross && ab_cross;
}
判断 c 是否与 ab 共线,可以通过 c 到直线 ab 的距离来判断,小于一个极小值就算共线
判断 c 是否在线段 ab 上则直接通过坐标计算即可
通过上面判断线段相交可以处理处理线段 af 与 gh 的情况,那么如何处理 ag 线段在多边形外的情况呢?
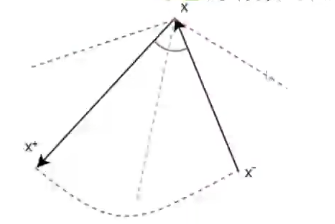
我们先定义什么是锥形
以上图为例,直线 (x, x-) 和 直线 (x, x+) 就可以构成一个锥形
我们先分类讨论,如果是凸点(小于 180° 角的点),那么对角线在锥形范围内;如果是凹点(大于 180° 角的点),那么对角线在锥形范围外
所以算法的重点在如何判断直线在锥形范围内
其实也很简单,如果点在锥形范围内,那么该点在 (x-, x) 线段左边,并且在 (x, x+) 线段左边
综合以上几种算法,我们可以检测对角线是否与非临边相交和对角线是否在锥形内部
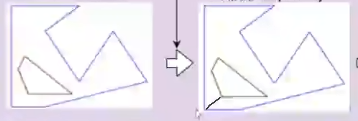
如果多边形内部存在 hole (洞),解决方法其实也很简单,将内部洞与外围点连接,将带空洞的多边形变为简单多边形,当然这个内部洞与外围的连接点也必须是互相可见的
上图连接的一根线,将带空洞的多边形变成了下图这种简单多边形,下图稍微夸张了一点分割部分,主要是为了强调这根线的作用
在 Recast Navigation 中,划分凸多边形使用的是耳切法(Ear Clipping),Meadow Mapping 划分凸多边形则使用的是二分法。耳切法使用更加聪明的方式,使得每个切出来的区域都是单独的三角形,避免 Meadow Mapping 递归调用的额外开销
Recast Navigation 是一种基于耳切法的划分算法,它的基本思想是从一个凸多边形的任意一个顶点开始,判断该顶点是否是一个耳朵,即该顶点的内角小于 180°,并且以该顶点为顶点的三角形不包含其他顶点。如果是耳朵,那么就将该顶点和相邻的两个顶点组成一个三角形,从多边形中切除该耳朵,否则就跳过该顶点,继续检查下一个顶点。重复上述过程,直到多边形被切割成若干个三角形为止。然后对每个三角形进行合并,使其满足最大顶点数的限制,得到最终的凸多边形集合。这种算法的优点是划分后的多边形的角度较大,有利于寻路效率,缺点是划分后的多边形数量较多,占用空间较大
寻路优化
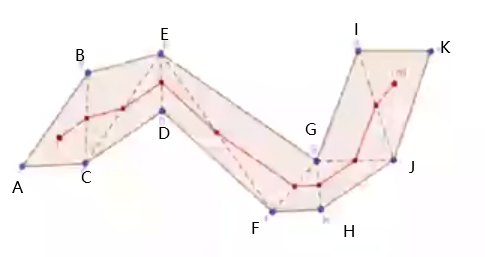
Meadow Mapping 采用 A* 算法进行寻路
很明显上面的路径并不是真实意义上的最短路径,以 DE 线段上的路径点为例,如果路径点在D上明显可以缩短路径
所以 Meadow Mapping 提出了一个路径改善算法,采用局部贪心的策略:遍历每个在边检中点的路径节点,考虑三种方案
- 保持路径在边界中点不变
- 选择边界左边节点
- 选择边界右边节点
针对以上三种方案,选择距离最短的路径
Recast Navigation在路径优化时使用String pulling漏斗算法
体素化
参考 Denis Haumont 在 2003 年发表的 Volumetric cell-and-portal generation,有三个重点:引入体素化去除高频细节;使用 Watershed 算法进行区域划分;引入距离场的概念
为什么要使用体素化?
在更多的材料中,体素化旨在处理 Polygon Soup (多边形大乱炖)问题。在面对若干 Mesh 时,体素化能将多个 Mesh 统一成一种表达
多边形大乱炖的意思是存在各种各样奇奇怪怪的多边形,它们互相组合成更多奇奇怪怪的多边形
体素化约占 Recast Navigation Build耗时的 80%~90%
UE 获取 Collision
对于 3D 场景来说,角色就是在一个碰撞体上移动,所以要获得可行走区域首先需要获得 Collision 数据
在 Unreal 游戏引擎中,最后都是调用 FRecastNavMeshGenerator::ExportRigidBodyGeometry() 接口,可能不同的版本可能会使用不同的物理引擎(比如 Chaos 和 PhysX),但是最后都是调用这个统一接口
大多数的碰撞器有不同的表现,可能是 Box、Sphere 等,这些东西最后都会被聚合起来变成 Vertex + Index 的性质
至于如何获取场景中的 Collision 数据,最简单的方法就是获得场景中所有的 Actor,遍历 Actor 上的 Component,将其与 Nav Mesh Bounds Volume 判断 AABB 碰撞,如果在范围内则导出该碰撞 Collision
由于场景中 Actor 可能非常多,直接遍历场景中所有 Actor 明显是非常浪费的
Unreal 会将所有的碰撞体维护在一颗八叉树中。将指定 Nav Mesh Bounds Volume 的 AABB 盒放入八叉树查询,找到与该 AABB 盒相交的所有碰撞体,体素化
八叉树维护内存成本高
小场景遍历可能更快,内存消耗更小
Unreal 中如何实现 Actor 移动出发导航网格更新的呢?
首先就是在 UNavigationSystemV1 绑定了组件移动的函数
UNavigationSystemBase::UpdateComponentDataAfterMoveDelegate().BindLambda([](USceneComponent& Comp) { UNavigationSystemV1::UpdateNavOctreeAfterMove(&Comp); });
在回调函数中会出发了 Octree 的更新
void UNavigationSystemV1::UpdateNavOctreeAfterMove(USceneComponent* Comp)
{
AActor* OwnerActor = Comp->GetOwner();
if (OwnerActor && OwnerActor->GetRootComponent() == Comp)
{
UpdateActorAndComponentsInNavOctree(*OwnerActor, true);
}
}
但是上面并不是直接更新八叉树的真实数据,而是将数据存储在 OctreeController.PendingOctreeUpdates 中
struct FNavigationOctreeController
{
enum EOctreeUpdateMode
{
OctreeUpdate_Default = 0, // regular update, mark dirty areas depending on exported content
OctreeUpdate_Geometry = 1, // full update, mark dirty areas for geometry rebuild
OctreeUpdate_Modifiers = 2, // quick update, mark dirty areas for modifier rebuild
OctreeUpdate_Refresh = 4, // update is used for refresh, don't invalidate pending queue
OctreeUpdate_ParentChain = 8, // update child nodes, don't remove anything
};
TSet<FNavigationDirtyElement> PendingOctreeUpdates;
TSharedPtr<FNavigationOctree, ESPMode::ThreadSafe> NavOctree;
/** Map of all objects that are tied to indexed navigation parent */
TMultiMap<UObject*, FWeakObjectPtr> OctreeChildNodesMap;
/** if set, navoctree updates are ignored, use with caution! */
uint8 bNavOctreeLock : 1;
// 一些其他函数
private:
static NAVIGATIONSYSTEM_API uint32 HashObject(const UObject& Object);
};
随后由 UWorld::Tick 调用 UNavigationSystemV1::Tick 来更新数据信息
void UWorld::Tick( ELevelTick TickType, float DeltaSeconds )
{
// Begin: 做一些事
// 调用 NavSystem 的 Tick
// update world's subsystems (NavigationSystem for now)
if (NavigationSystem != nullptr)
{
SCOPE_CYCLE_COUNTER(STAT_NavWorldTickTime);
CSV_SCOPED_TIMING_STAT_EXCLUSIVE(NavigationBuild);
NavigationSystem->Tick(DeltaSeconds);
}
// After: 做一些事
}
void UNavigationSystemV1::Tick(float DeltaSeconds)
{
// Begin: 做一些事情
// 如果 PendingOctreeUpdates 不为空,更新 NacOctree
if (DefaultOctreeController.PendingOctreeUpdates.Num() > 0)
{
FNavigationDataHandler NavHandler(DefaultOctreeController, DefaultDirtyAreasController);
NavHandler.ProcessPendingOctreeUpdates();
}
// After: 做一些事情
}
// 遍历 PendingOctreeUpdates 所有对象,将其添加到 NavOctree 中
void FNavigationDataHandler::ProcessPendingOctreeUpdates()
{
QUICK_SCOPE_CYCLE_COUNTER(STAT_Navigation_ProcessPendingOctreeUpdates);
if (OctreeController.NavOctree)
{
// AddElementToNavOctree (through some of its resulting function calls) modifies PendingOctreeUpdates so invalidates the iterators,
// (via WaitUntilAsyncPropertyReleased() / UpdateComponentInNavOctree() / RegisterNavOctreeElement()). This means we can't iterate
// through this set in the normal way. Previously the code iterated through this which also left us open to other potential bugs
// in that we may have tried to modify elements we had already processed.
while (TSet<FNavigationDirtyElement>::TIterator It = OctreeController.PendingOctreeUpdates.CreateIterator())
{
FNavigationDirtyElement Element = *It;
It.RemoveCurrent();
AddElementToNavOctree(Element);
}
}
OctreeController.PendingOctreeUpdates.Empty(32);
}
为什么不直接更新 NavOctree 中的数据呢?
因为一次更新 NavOctree 的性能消耗是很大的,所以收集一次信息后统一更新。可以将多个更新请求进行合并和优化,避免频繁地修改 NavOctree 的结构,从而提高性能和稳定性
在 AddNode 的时候才真正收集碰撞体数据到 NavOctree 中
OctreeController.NavOctree->AddNode(ElementOwner, DirtyElement.NavInterface, ElementBounds, GeneratedData);
OctreeController.NavOctree->AppendToNode(*ElementId, DirtyElement.NavInterface, ElementBounds, GeneratedData);
体素化
相关功能在 Engine\Source\Runtime\Navmesh\Private\Recast\RecastRasterization.cpp 文件中
把世界理解成一个 Minecraft 的世界,整个世界都是由一个一个方块组成的
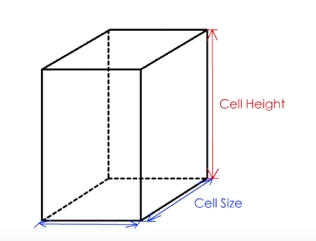
每个体素由长方体构成,水平面上为正方形
至于为什么不是正方体,是因为对于大多数用于行走的 NevMesh 来说对于高度的精度要求没有水平面那么高,所以很多时候 Cell Height 会比 Cell Size 大很多
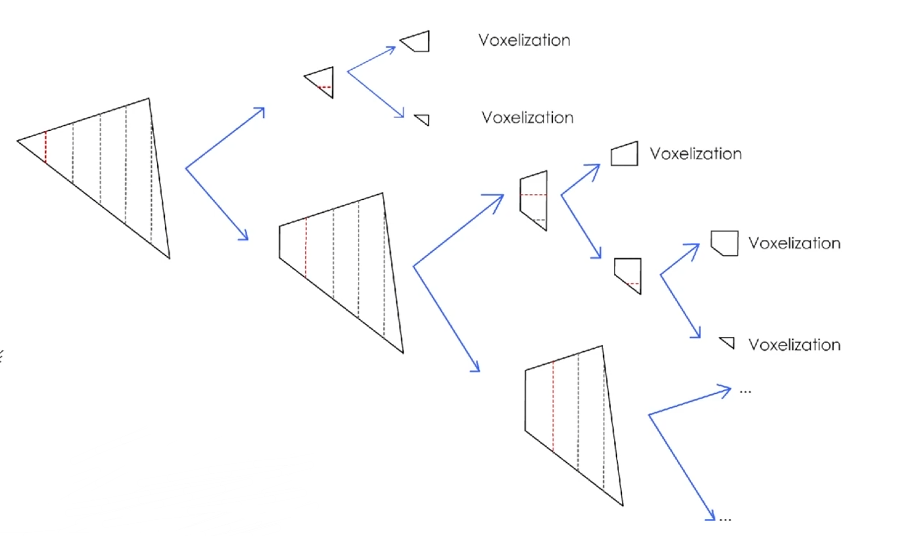
体素化实现过程
- 遍历所有偶碰撞器每个三角面
- 沿水平面垂直(y轴)切分 (以
Cell Size切分) - 沿水平面水平(x轴)七分 (以
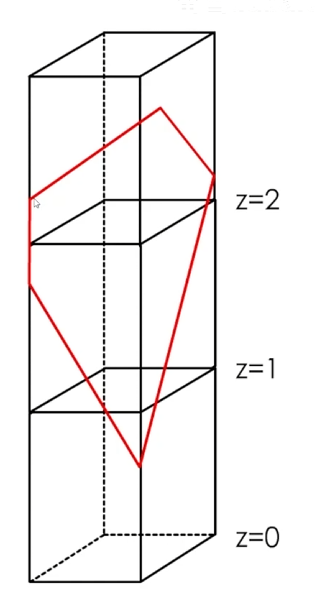
Cell Size切分) - 将切分下来的多边形体素化(水平面切分后能保证在一个 Cell 里,这时根据多边形 z 值最大最小值,覆盖所有经过的体素)
上图为俯视角查看 Collision 的一个三角面,首先将三角面沿 y 轴切分,然后沿着 x 轴切分
最后得到多个小块,根据小块上点的 z 轴的最大值和最小值和 Cell Height 可以计算出该占据的体素
对应的代码如下
/// @par
///
/// No spans will be added if the triangle does not overlap the heightfield grid.
///
/// @see rcHeightfield
void rcRasterizeTriangle(rcContext* ctx, const rcReal* v0, const rcReal* v1, const rcReal* v2,
const unsigned char area, rcHeightfield& solid,
const int flagMergeThr, const int rasterizationFlags, const int* rasterizationMasks) //UE
{
rcAssert(ctx);
ctx->startTimer(RC_TIMER_RASTERIZE_TRIANGLES);
const rcReal ics = 1.0f/solid.cs;
const rcReal ich = 1.0f/solid.ch;
rasterizeTri(v0, v1, v2, area, solid, solid.bmin, solid.bmax, solid.cs, ics, ich, flagMergeThr, rasterizationFlags, rasterizationMasks); //UE
ctx->stopTimer(RC_TIMER_RASTERIZE_TRIANGLES);
}
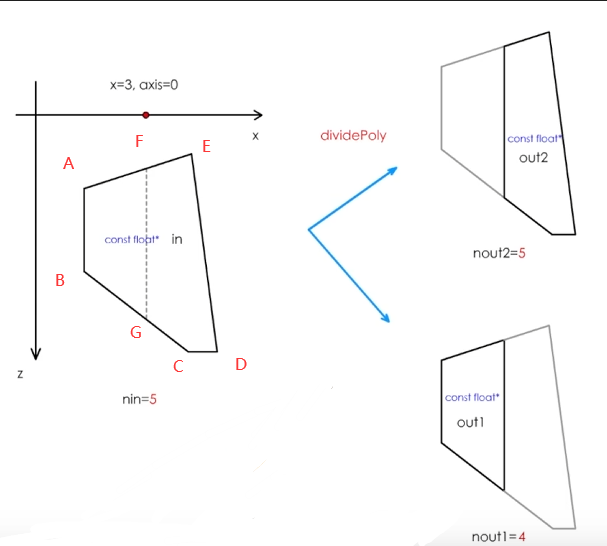
切割多边形算法函数为 static int clipPoly,旧版本是 static void dividePoly
算法的核心思路是逆时针遍历节点
对于 AE 来说,点 A 和点 E 在轴两边,所以 A 加入左边多边形,E 加入右边多边形,根据轴的坐标线性插值计算出 F 的坐标,同时加入左右两个多边形
对于 AB 来说,点 A 和点 B 在轴的左边,所以两个点都加入左边多边形
对于 BC 来说,点 B 和点 C 在轴两边,所以 B 加入左边多边形,C 加入右边多边形,根据轴的坐标线性插值计算出 G 的坐标,同时加入左右两个多边形
static int clipPoly(const rcReal* in, int n, rcReal* out, rcReal pnx, rcReal pnz, rcReal pd)
{
rcReal d[12];
for (int i = 0; i < n; ++i)
d[i] = pnx*in[i*3+0] + pnz*in[i*3+2] + pd;
int m = 0;
for (int i = 0, j = n-1; i < n; j=i, ++i)
{
bool ina = d[j] >= 0;
bool inb = d[i] >= 0;
if (ina != inb)
{
rcReal s = d[j] / (d[j] - d[i]);
out[m*3+0] = in[j*3+0] + (in[i*3+0] - in[j*3+0])*s;
out[m*3+1] = in[j*3+1] + (in[i*3+1] - in[j*3+1])*s;
out[m*3+2] = in[j*3+2] + (in[i*3+2] - in[j*3+2])*s;
m++;
}
if (inb)
{
out[m*3+0] = in[i*3+0];
out[m*3+1] = in[i*3+1];
out[m*3+2] = in[i*3+2];
m++;
}
}
return m;
}
最后将多边形所接触到的区域全部标记为占有,如下图所示
体素化表达
aaabbbbccc 可以表达为 3a4b3c,在运行时再解压缩成真正的字符串,这种方法被称为 Run-length encoding
同理,对于体素来说也可以这么做
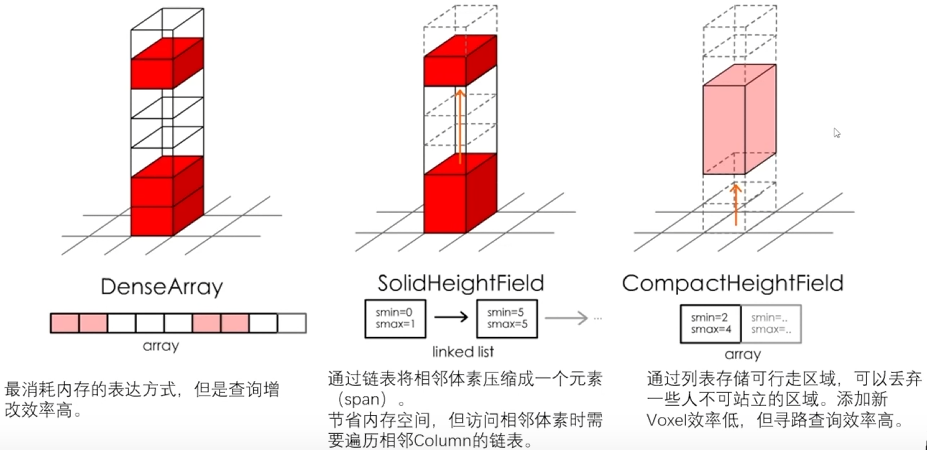
如果直接使用数组存储体素是比较占用内存的,所以可以先将相邻的体素压缩成一个 span,这个时候存储的是被占用的体素,可以将 SolidHeightField 转换成存储不被占用的体素,即 CompactHeightField
一般来说 CompactHeightField 存储的就是可行走区域,这种存储结构可以让寻路效率增加,但是如果增减体素则效率低
设定人体需要占用两个
Cell Height,所以最上面的体素是不能站人的,因此在CompactHeightField中被剔除
上面三种数据结构 DenseArray、SolidHeightField 和 CompactHeightField 在不同情况各有优势
DenseArray访问修改体素状态快、查询寻路慢、内存占用高SolidHeightField内存占用小、访问修改体素状态速度中、查询寻路速度中CompactHeightField内存占用小、访问修改体素修改速度慢、查询寻路速度快
在不同的应用情况,可以考虑使用不同的数据结构存储体素信息