MarkdownLog/AI/漏斗算法

漏斗算法

文章：https://blog.csdn.net/fengkeyleaf/article/details/118832924

在导航网格中

1. 通过凸包和三角形划分，能够得到有关联关系的多边形数组
2. 通过 A* 寻路算法，能够得到从起点到目标点会经过的多边形数组

需要通过多边形数组来定位需要经过的路径

一般是会切割成多个三角形不会出现多边形。因为当玩家进入一个三角形的时候，一个边是玩家的入口，另一个边是障碍物，最后只有一个边是出口，比较明确出入关系

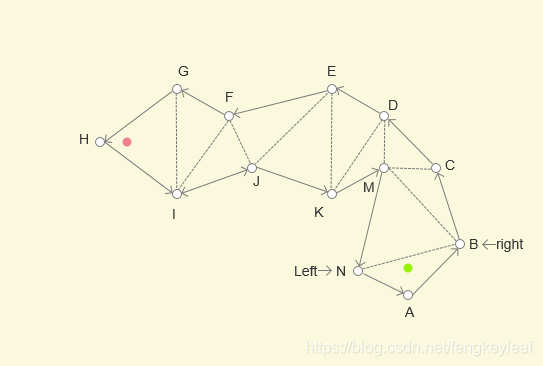
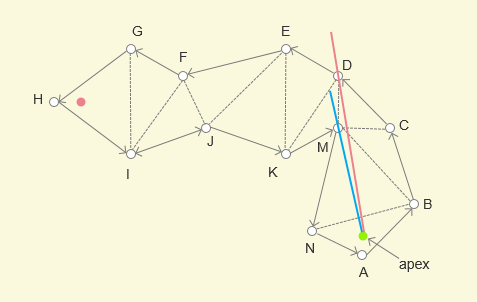
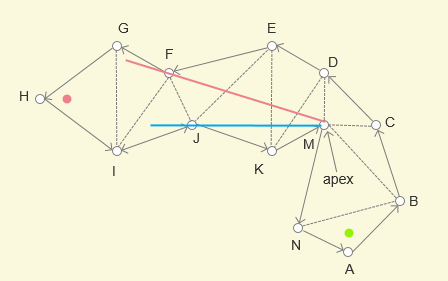
绿点作为起点，红点作为终点，如何找到一条最短路径能够从起点到终点呢？

设定 绿点 为 X，红点为 Y

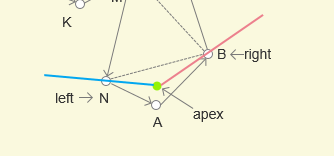
绿点作为起点，被包括在三角形 ABN 中，首先定位到下一个三角形是 NMB，那么公共边 NB 是一定要经过的，所以将 XN 作为左边界，XB 作为右边界，形成一个漏斗形状

漏斗算法计算流程就是下面两步交替运行

1. 如果新的顶点与 判定点 形成的漏斗比原来的小，那么将对应的左顶点或者右顶点移动到该位置；反之不做更新
2. 如果新的一侧顶点与 判定点 形成的边界，越过了另一侧原顶点与 判定点 形成的边界，则将另一侧原顶点设置新的 判定点，并将该点添加到最路径中

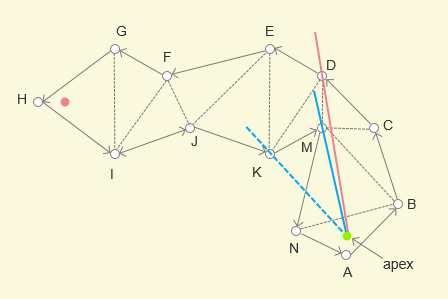
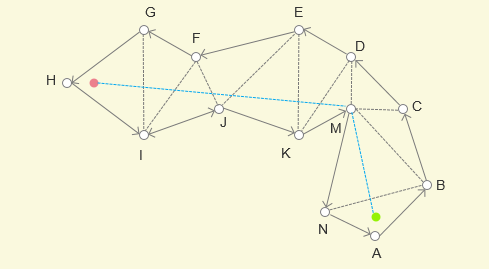
根据上图所示的情况，进行实际分析

1. 对于 N 和 B 两点，B点在下一个三角形 BCM 边界上，N 没有，所以先动 左边界 XN，左边界变成 XM
2. 由于新边界 XM 和 XB 形成的漏斗比原来小，则 XM 形成新边界

1. 再动右边界，从 XB 变更为 XC，由于 XM 和 XC 形成的漏斗更小，所以右边界变更为 XC

1. 再判断 M 和 C 两点，由于 M 在下一个三角形 KMD 边界上，所以先动 C 点，也就是右边界
2. 由于新右边界 XD 和 XM 形成的漏斗更小了，所以右边界更新为 XD

1. 更新左边界，XM 更新为 XK，由于 XK 和 XD 形成的漏斗变大了，所以 XK 更新失败，退回到 XM

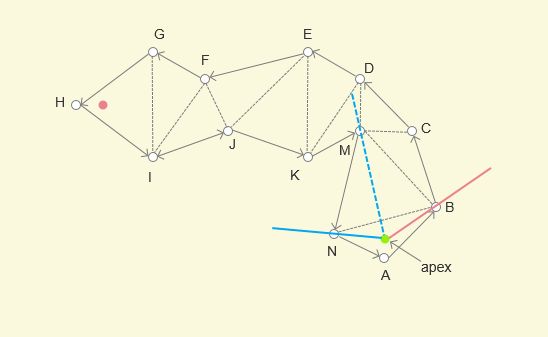
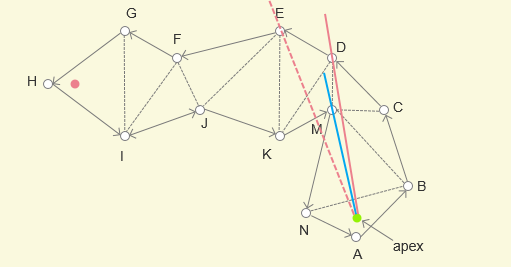
1. 更新右边界，由于右边界 XE 超过了左边界 XM，所以更新目标点，从 X 点变为 M 点，并将 M 点添加到最短路径中

1. 以 M 点作为新的判定点，重新设置漏斗

1. 将右边界从 MD 更新为 ME，角度减少，右边界更新成功，变为 ME
2. 将左边界从 MK 更新为 MJ，角度减少，左边界更新成功，变为 MJ
3. 将右边界从 ME 更新为 MF，角度减少，右边界更新成功，变为 MF
4. 将左边界从 MJ 更新为 MI，角度增加，左边界更新失败，保持为 MJ
5. 将右边界从 MF 更新为 MG，角度增加，右边界更新失败，保持为 MF
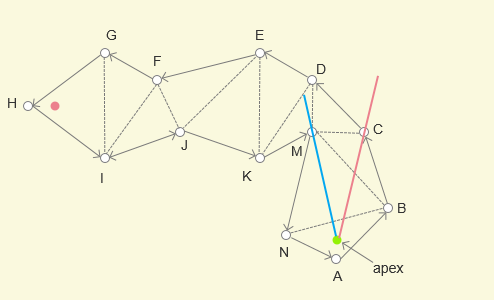
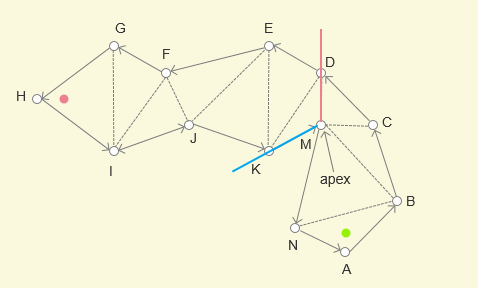
6. 将左边界从 MJ 更新为 MY (Y是终点)，角度减少，左边界更新成功
7. 将右边界从 MF 更新为 MY (Y是终点)，角度减少，右边界更新成功
8. 左右边界都是 MY，漏斗算法结束

那么最短路径也就确定了，从 X(起点) -> M -> Y(终点)

补充说明

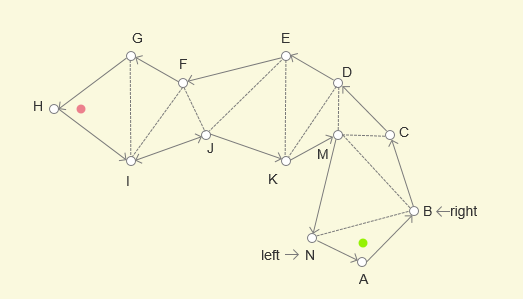
以 N 点为例，规定其为左边界顶点，那么沿着多边形的外边(实线边)，所经过的顶点都是左边界顶点，不包括 H

同理，B 为右边界顶点，那么 B、C、D、E、F、G 也都是右边界顶点

通过，这个规则，确定了左边界顶点和右边界顶点

那么，每次更新顶点的时候是先更新左顶点还是右顶点呢？

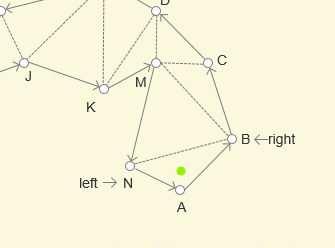
由于所有都是三角形，并且每个三角形只有一个相邻的三角形，所以所以三角形中一定存在一个导航边，和一个外边

以上图为例，BM 作为连接 MCB 和 NMB 的边是导航边，那么另一个边 MN 就是外边

同理，对于三角形 MCD 来说，MD 是导航边，CD 是外边