为什么要学习计算机图形学？——计算机图形学就是厉害

图形学是非常广阔的世界

前提知识

基础数学
基础物理
信号处理
数值分析
美学
……

线性代数

向量、矩阵的操作，点乘、叉乘、矩阵乘法等

点乘

$$ \vec{A} = (^{x} _{y}) \ \vec{A}^T = (x, y) \ \lVert \vec{A} = \sqrt{x ^2 + y^2} \rVert \ $$

向量之间的点乘

$$ \vec{A} \cdot \vec{B} = \lVert \vec{A} \rVert * \lVert \vec{B} \rVert * \cos \theta \ \cos \Theta = \frac{\vec{A} \cdot \vec{B}}{\lVert \vec{A} \rVert * \lVert \vec{B} \rVert} $$

向量点乘的数学运算规则

交换律：$\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}$
分配律：$\vec{a} \cdot (\vec{b} + \vec{c}) = \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c}$
结合律：$(k*\vec{a}) \cdot \vec{b} = \vec{a} \cdot (\vec{b} * k) = k * (\vec{a} \cdot \vec{b})$

点乘的运算

2D： $\vec{a} \cdot \vec{b} = (^{x_a} _{y_a}) \cdot (^{x_b} _{y_b}) = x_a*x_b + y_a*y_b $
3D： $\vec{a} \cdot \vec{b} = \begin{pmatrix}x_a \ y_a \ z_a\end{pmatrix} \cdot \begin{pmatrix} x_b \ y_b \ y_c \end{pmatrix} = x_a * x_b + y_a * y_b + z_a * z_b$

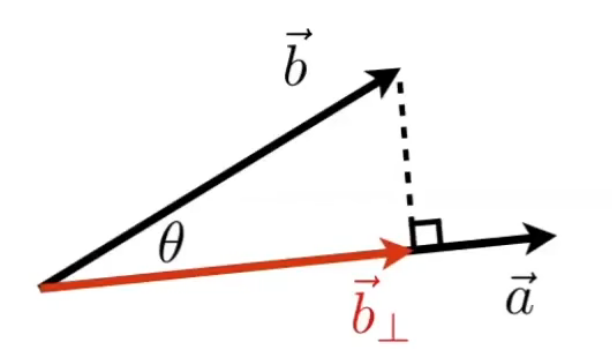
$$ \vec{b{\bot}} = \lVert \vec{b\bot} \rVert = \lVert \vec{b} \rVert * \cos \Theta $$

方向大致相同：$\cos{(\vec{a} \backsim \vec{b})} < 0$
方向不同：$\cos{(\vec{a} \backsim \vec{c})} > 0$

向量点乘的作用(单位向量)
- 通过点乘的运算，可以找到两个方向之间的余弦夹角
- 找到一个向量投影到另一个向量中，也会用到点乘运算
- 判断两个向量是否接近，通过值的大小比较即可（cos在0~$\pi$单调递减）
- 关于是否同方向的信息（$\cos \theta$小于$90°$大于0，否则小于0）

叉乘

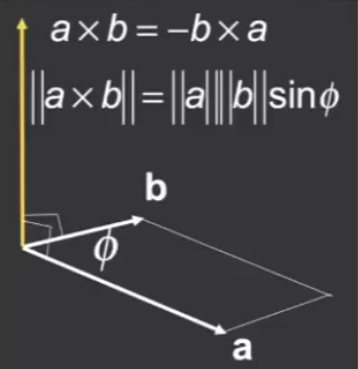
两个向量叉乘的结果是垂直于当前两个向量所在平面的新的向量

$$ \vec{a} \times \vec{b} = -\vec{b} \times \vec{a}\ \lVert \vec{a} \times \vec{b} \rVert = \lVert \vec{a} \rVert * \lVert \vec{b} \rVert * \sin{\Theta} $$

叉乘的运算需要用到右手螺旋法则，$\vec{a} \times \vec{b}$就是四指从$\vec{a}$到$\vec{b}$，那么大拇指的指向就是$\vec{c}$所在的方向

叉乘的一些数学运算规律

叉乘没有交换律
叉乘有分配律
叉乘有结合律

$$ \vec{x} \times \vec{y} = + \vec{z}\ \vec{y} \times \vec{x} = - \vec{z}\ \vec{y} \times \vec{z} = + \vec{x}\ \vec{z} \times \vec{y} = - \vec{x}\ \vec{z} \times \vec{x} = + \vec{y}\ \vec{z} \times \vec{x} = - \vec{y}\ \vec{a} \times \vec{b} = -\vec{b} \times \vec{a}\ \vec{a} \times \vec{a} = \vec{0}\ \vec{a} \times (\vec{b} + \vec{c}) = \vec{a} \times \vec{b} + \vec{a} \times \vec{c}\ \vec{a} \times (k * \vec{b}) = k * (\vec{a} \times \vec{b})\ $$

上述所有都基于右手坐标系
叉乘没有交换律

叉乘的数学计算方式

$$ \vec{a} \times \vec{b} = \begin{pmatrix}

y_a * z_b - y_b * z_a \\
z_a * x_b - x_a * z_b \\
x_a * y_b - y_a * x_b \\

\end{pmatrix} $$

叉乘的作用
- 判断左右(根据右手螺旋法则)
- 判断内外(点是否在三角形内的叉乘解法)

矩阵

矩阵和一个数相乘

$$ k * \begin{pmatrix}

x & a \\ 
y & b \\
z & c \\

\end{pmatrix} = \begin{pmatrix}

k*x & k*a \\ 
k*y & k*b \\
k*z & k*c \\

\end{pmatrix} $$

矩阵和一个矩阵相乘

A矩阵的列数必须等于B矩阵的行数

$\left( M \times N \right) * \left( N \times P \right) = \left( M \times N \right)$公式中$\left( M \times N \right)$表示M行、N列的矩阵

$$ \begin{pmatrix}

x_1 & a_1 \\ 
y_1 & b_1 \\
z_1 & c_1 \\

\end{pmatrix}* \begin{pmatrix}

x_2 & a_2 & q_2 & e_2 \\ 
y_2 & b_2 & w_2 & r_2 \\

\end{pmatrix}= \begin{pmatrix}

x_1 * x_2 + a_1 * y_2 & x_1 * a_2 + a_1 * b_2 & x_1 * q_2 + a_1 * w_2 & x_1 * e_2 + a_1 * r_2 \\ 
y_1 * x_2 + b_1 * y_2 & y_1 * a_2 + b_1 * b_2 & y_1 * q_2 + b_1 * w_2 & y_1 * e_2 + b_1 * r_2 +\\
z_1 * x_2 + c_1 * y_2 & z_1 * a_2 + c_1 * b_2 & z_1 * q_2 + c_1 * w_2 & z_1 * e_2 + c_1 * r_2 \\

\end{pmatrix} $$

矩阵的数学规律
- 矩阵没有交换律
- 矩阵有结合律$(AB)C = A(BC)$
- 矩阵具有分配律$A(B+C) = AB + AC$

当矩阵与向量相乘时，一般将矩阵放在左边，向量放在右边，向量可以看作是(M, 1)的矩阵，那么左边的矩阵只要是M列就行

将单位向量按y轴对称的操作： $$ \begin{bmatrix}

-1 & 0 \\
0 & 1

\end{bmatrix} * \begin{bmatrix}

x\\
y

\end{bmatrix}= \begin{bmatrix}

-x \\
y

\end{bmatrix} $$

矩阵的转置:行和列互换

$$ \begin{bmatrix}

1 & 2 \\
3 & 4 \\
5 & 6

\end{bmatrix} ^T = \begin{bmatrix}

1 & 3 & 5 \\
2 & 4 & 6

\end{bmatrix} \ (AB)^T = B^T * A^T $$

单位矩阵:主对角线上是1，其他地方都是0

$$ I_{3\times3} = \begin{bmatrix}

1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1

\end{bmatrix} $$

矩阵的逆：矩阵A乘矩阵B得到单位矩阵，则成B是A的逆，写作$A^{-1}$

$AA^{-1} = I$、$(AB)^{-1} = B^{-1} * A^{-1}$

向量的点乘转成矩阵运算

$$ \vec{a} \cdot \vec{b} = \vec{a}^T\vec{b}= \begin{bmatrix}

x_a & y_a & z_a

\end{bmatrix} \begin{bmatrix}

x_b \\ y_b \\ z_b

\end{bmatrix}= \left( x_a*x_b + y_a*y_b + z_a*z_b \right) $$

向量的叉乘转成矩阵运算

$$ \vec{a} \times \vec{b} = A^*\vec{b} = \begin{bmatrix}

0 & -z_a & y_a \\
z_a & 0 & -x_a \\
-y_a & x_a & 0

\end{bmatrix} \begin{bmatrix}

x_b \\ y_b \\ z_b

\end{bmatrix} $$

$A^*$是$\vec{a}$的dual matrix

变换

仿射变换

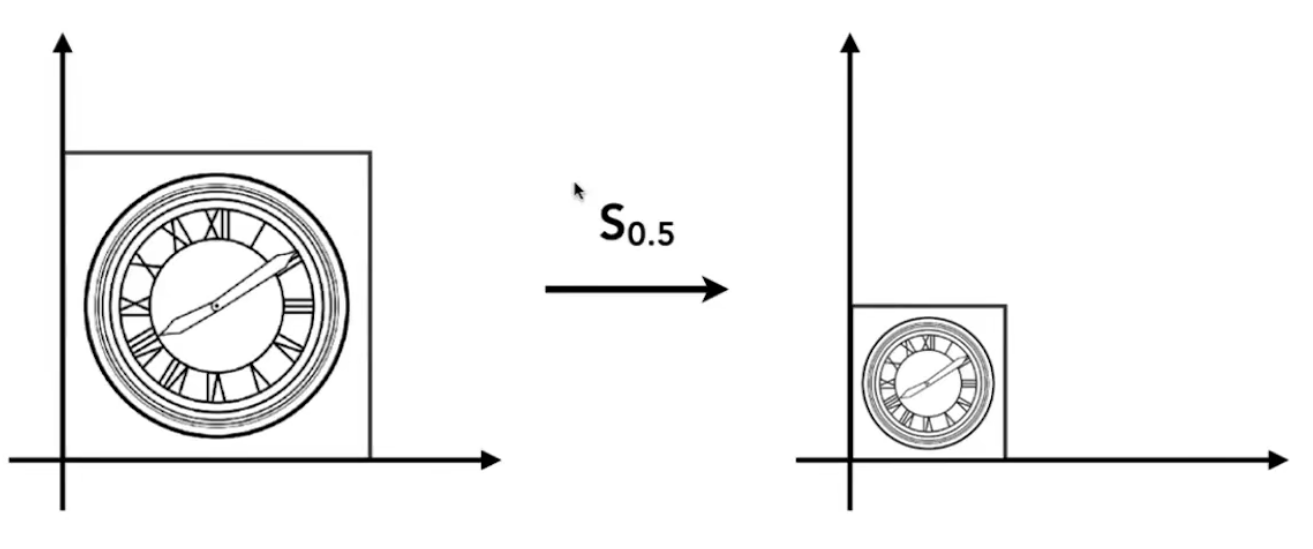
伸缩变换(Scale)

$$ x' = sx\ y' = sy\ \Rightarrow \ \begin{bmatrix}

x' \\ y'

\end{bmatrix}= \begin{bmatrix}

s & 0 \\
0 & s

\end{bmatrix} \begin{bmatrix}

x \\ y

\end{bmatrix} $$

镜像

$$ x' = -x\ y' = y\ \Rightarrow \ \begin{bmatrix}

x' \\ y'

\end{bmatrix}= \begin{bmatrix}

-1 & 0 \\
0 & 1

\end{bmatrix} \begin{bmatrix}

x \\ y

\end{bmatrix} $$

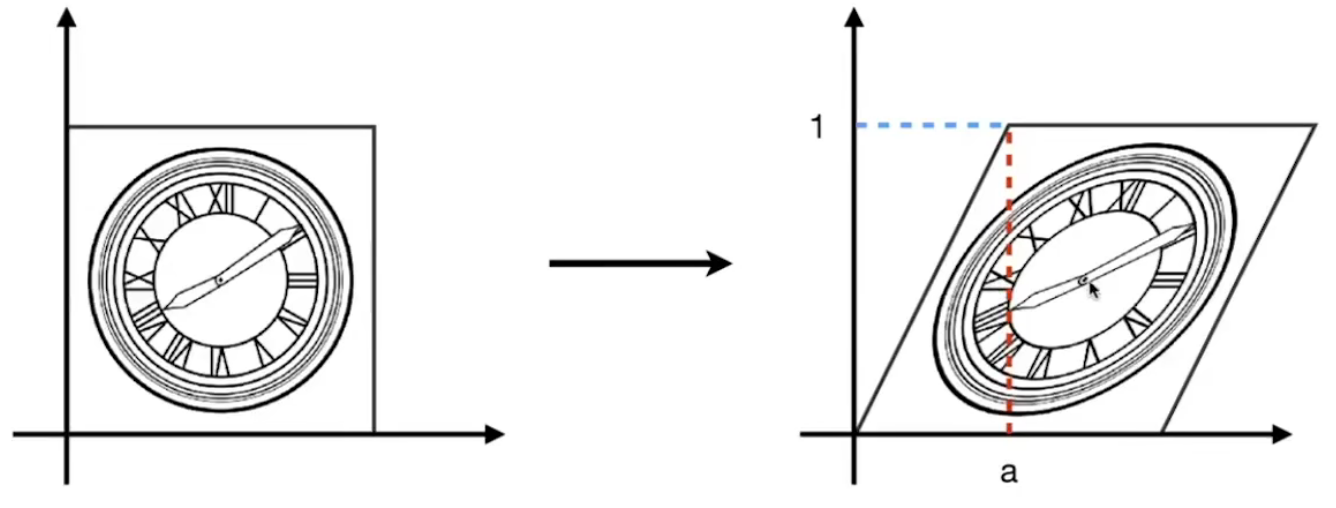
切变

$$ x' = x + a*y\ y' = y\ \Rightarrow \ \begin{bmatrix}

x' \\ y'

\end{bmatrix}= \begin{bmatrix}

1 & a \\
0 & 1

\end{bmatrix} \begin{bmatrix}

x \\ y

\end{bmatrix} $$

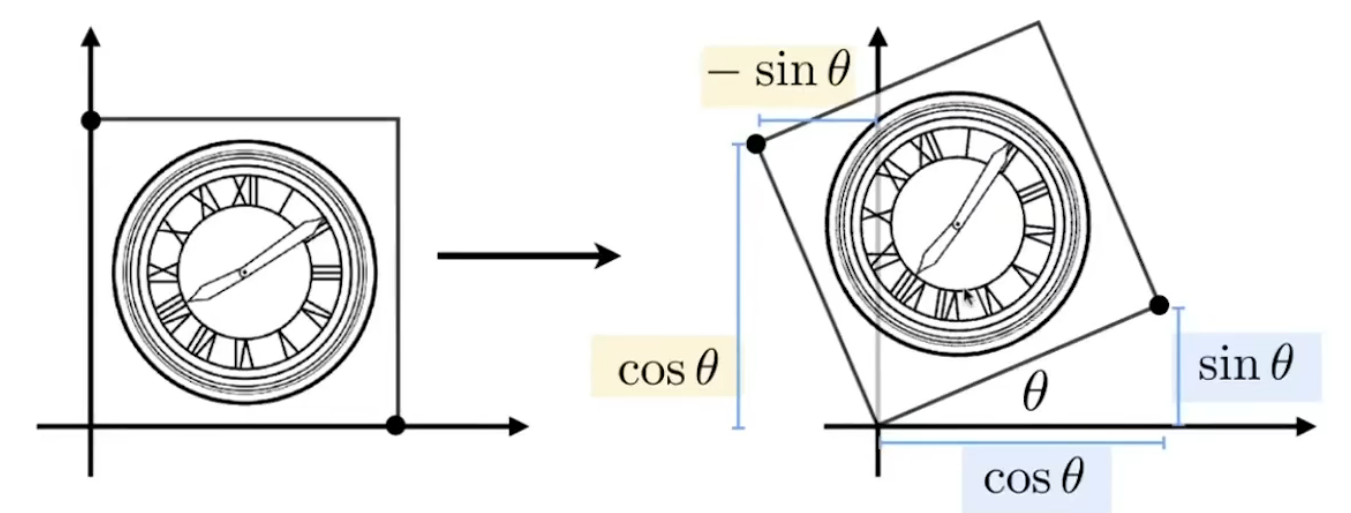
旋转(Rotate)

默认绕原点逆时针旋转

公式推导

右下角点坐标(1, 0)=>($\cos\Theta, \sin\Theta$)
左上角点坐标(0, 1)=>($-\sin\Theta, \cos\Theta$)

$$ \left(x', y'\right) \Longrightarrow \begin{bmatrix}

A & B \\
C & D

\end{bmatrix} \begin{bmatrix}

x \\ y

\end{bmatrix}\ 带入x=1, y=0, x'=\cos\Theta, y'=\sin\Theta\ 得: A = \cos\Theta , C = \sin\Theta\ 带入x=0, y=1, x'=-\sin\Theta, y'=\cos\Theta\ 得: B = -\sin\Theta, D = \cos\Theta $$

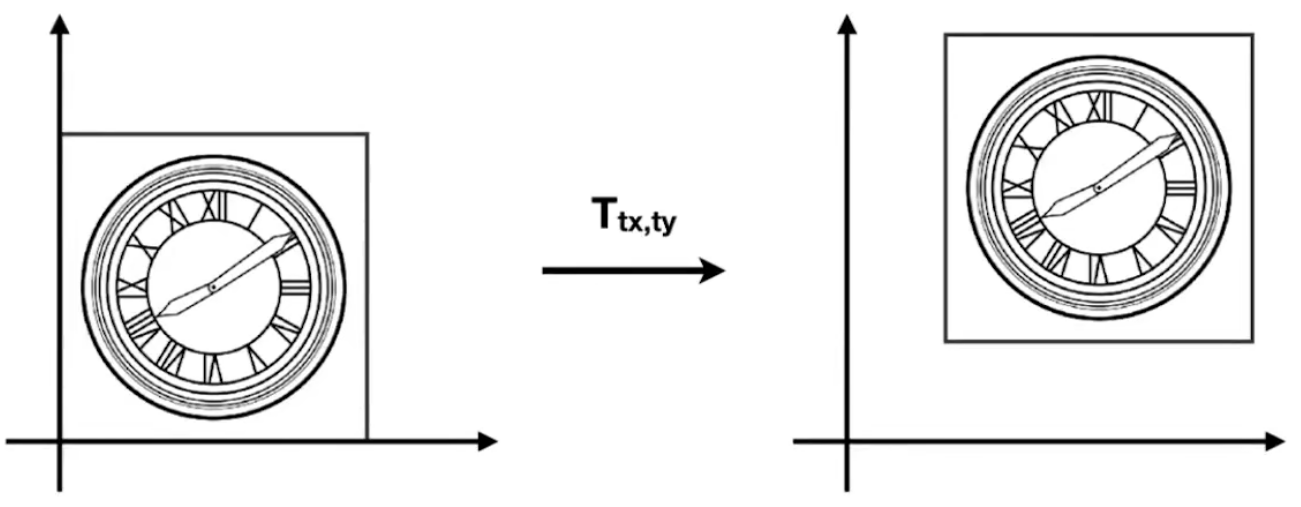
平移(Transiation)

$x' = x + t_x$
$y' = y + t_y$

$$ \begin{bmatrix}

x' \\ y ^ `

\end{bmatrix}= \begin{bmatrix}

1 & 0 \\
0 & 1

\end{bmatrix} \begin{bmatrix}

x \\ y

\end{bmatrix}+ \begin{bmatrix}

t_x \\ t_y

\end{bmatrix} $$

很明显，这个平移的坐标无法通过一个矩阵就表示出来，这个时候就需要引入齐次矩阵

齐次矩阵就是将一个原本是n维的向量用一个n+1维向量来表示

$$ \begin{bmatrix}

x' \\ y ^ ` \\ 1

\end{bmatrix}= \begin{bmatrix}

1 & 0 & t_x \\
0 & 1 & t_y \\
0 & 0 & 1

\end{bmatrix} \begin{bmatrix}

x \\ y \\ 1

\end{bmatrix}= \begin{bmatrix}

x + t_x \\ y + t_y \\ 1

\end{bmatrix} $$

通过齐次坐标矩阵就可以使用一个矩阵来表示线性变换，为了保证变换矩阵的一致性，所以上面讲的所有矩阵都需要转换成齐次矩阵

在其次坐标中，点使用$\begin{pmatrix}

x \\ y \\ 1

\end{pmatrix}$ 来表示，向量使用$\begin{pmatrix}

x \\ y \\ 0

\end{pmatrix}$ 来表示

向量 + 向量 = 向量
point - point = 向量
point + vector = point
point + point = 两点的中点

为什么point + point的结果是两个点的中点

$$ A = \begin{pmatrix}

x \\ y \\ w

\end{pmatrix}= \begin{pmatrix}

x / w \\ y / w \\ 1

\end{pmatrix} \ B = \begin{pmatrix}

a \\ b \\ c

\end{pmatrix}= \begin{pmatrix}

a / c \\ b / c \\ 1

\end{pmatrix} \ A + B = \begin{pmatrix}

x/w + a/c \\ y/w + b/c \\ 2

\end{pmatrix}= \begin{pmatrix}

\frac{x}{2w} + \frac{a}{2c} \\
\frac{y}{2w} + \frac{b}{2c} \\
1

\end{pmatrix} $$

总和

$$ Scale \Longrightarrow S(s_x, s_y) = \begin{pmatrix}

s_x & 0 & 0 \\
0 & s_y & 0 \\
0 & 0 & 1

\end{pmatrix} \ Rotation \Longrightarrow R(\Theta) = \begin{pmatrix}

\cos\Theta & -\sin\Theta & 0 \\
\sin\Theta & \cos\Theta & 0 \\
0 & 0 & 1

\end{pmatrix} \ Translation \Longrightarrow T(t_x, t_y) = \begin{pmatrix}

1 & 0 & t_x \\
0 & 1 & t_y \\
0 & 0 & 1

\end{pmatrix} $$

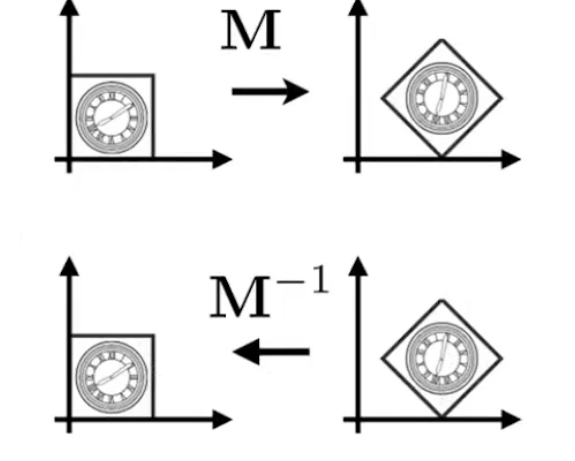
逆变换

逆变换就是把之前的操作反向来一次，对应的就是矩阵中的逆矩阵

组合变换

图1
图2

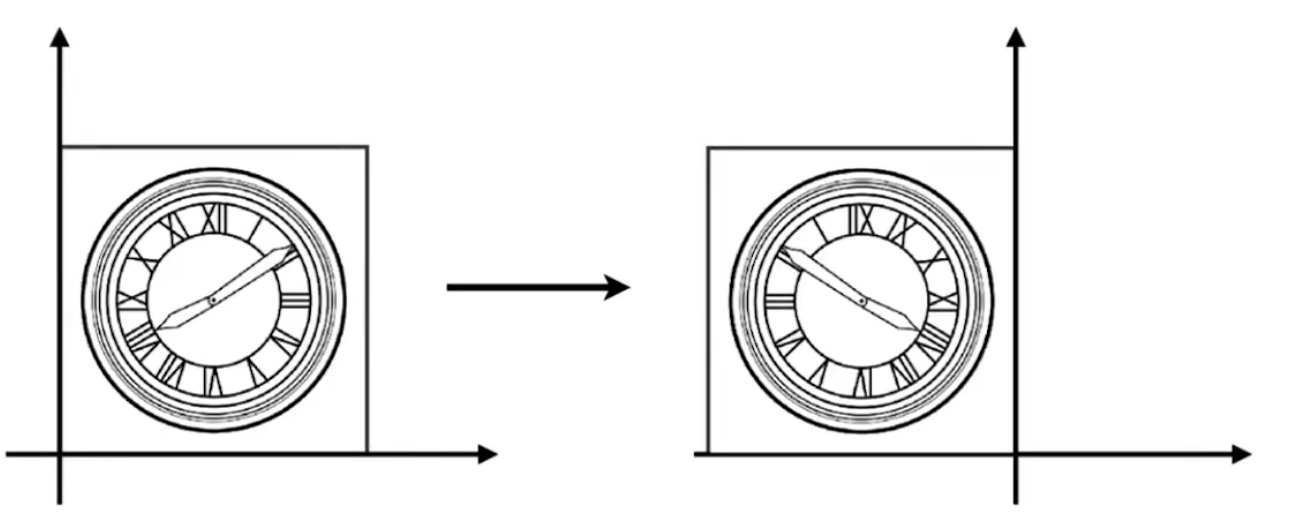
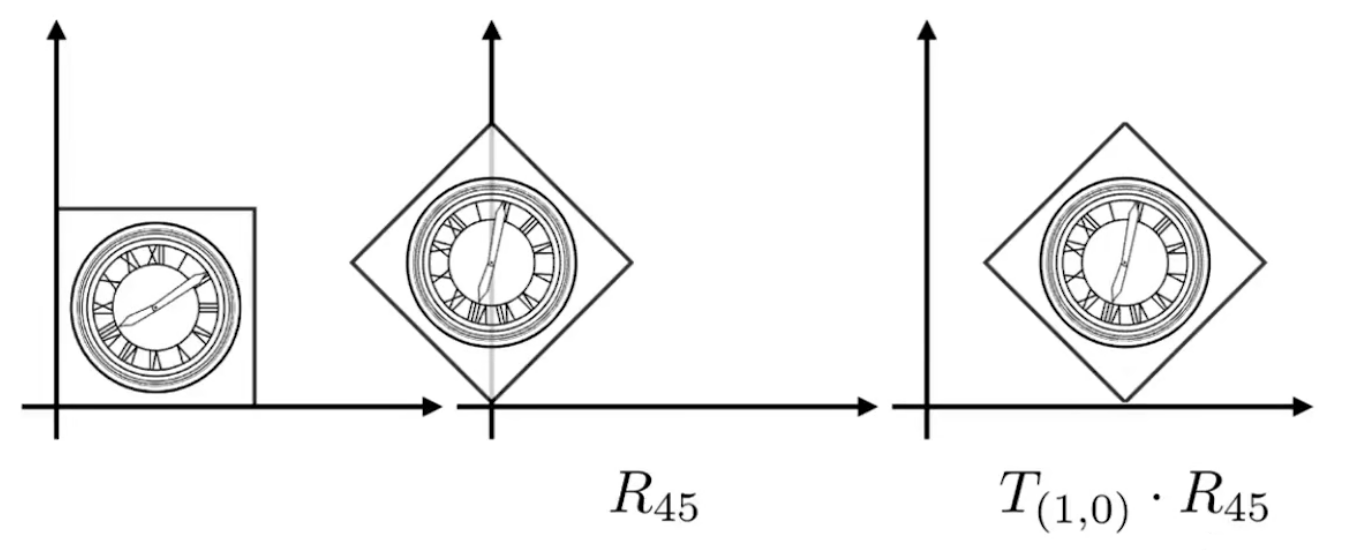
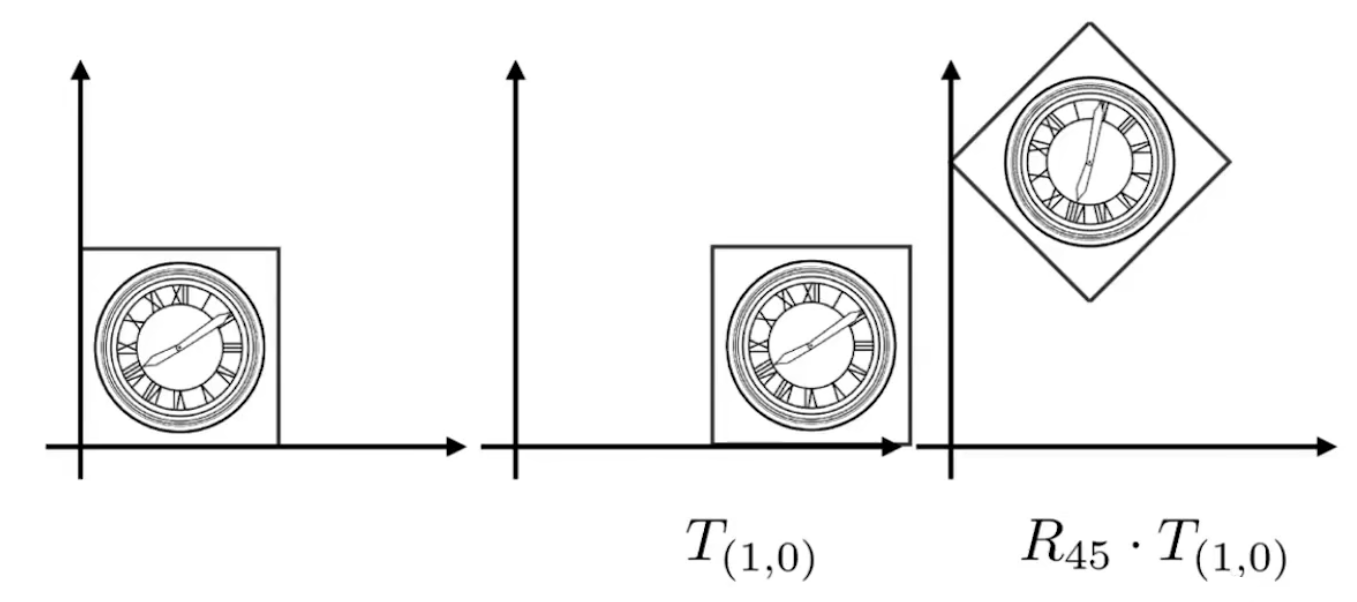
旋转默认绕原点，逆时针旋转

比较上述两张图片，可以发现先旋转再平移与先平移再旋转得到的结果是不同的，对应的理解就是矩阵的乘法，矩阵乘法不满足交换律

为了得到图1的效果，我们需要先旋转45°，再向X轴正方向平移1一个单位

$$ T{(1， 0)} \cdot R{45} \cdot \begin{bmatrix}

x \\ y \\ 1

\end{bmatrix}= \begin{bmatrix}

1 & 0 & 1 \\
0 & 1 & 0 \\
0 & 0 & 1

\end{bmatrix} \begin{bmatrix}

\cos45° & -\sin45° & 0 \\
\sin45° & \cos45° & 0 \\
0 & 0 & 1

\end{bmatrix} \begin{bmatrix}

x \\ y \\ 1

\end{bmatrix} $$

前面提过向量一般放在矩阵乘法的最右边，并且根据矩阵具有结合律，上述式子可以理解为先计算$R{45}$与$\begin{bmatrix}x\y\1\end{bmatrix}$，再计算与$T{(1, 0)}$的乘法

但是，根据矩阵的结合律，我们可以先把前面的矩阵的计算结果得出最终变换矩阵，最后与向量相乘

$$ A_n(...A_2(A_1(X)) = \underbrace{A_n...A_2 \cdot A1}{先计算} \cdot \begin{pmatrix}

x \\ y \\ 1

\end{pmatrix} $$

变换的分解

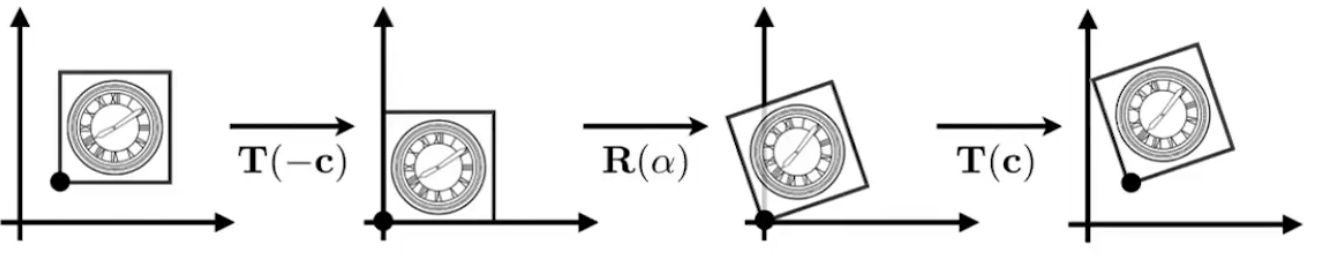
如果想让图片围绕左下角旋转，而不是原点选择，可以采用的解法是

左下角移动到原点 => 绕原点旋转 => 左下角移动到起始位置

三位空间的变换

三维与二维无非就是多了一个维度，其他的变换相似，原理相同

point : $\begin{pmatrix}

x & y & z & 1

\end{pmatrix}^T$
vector : $\begin{pmatrix}

x & y & z & 0

\end{pmatrix}^T$

$$ \begin{pmatrix}

x' \\ y^1 \\ z' \\ 1

\end{pmatrix}= \begin{pmatrix}

a & b & c & t_x \\
d & e & f & t_y \\
g & h & i & t_z \\
0 & 0 & 0 & 1

\end{pmatrix} \begin{pmatrix}

x \\ y \\ z \\ 1

\end{pmatrix} \ Scale \Longrightarrow S(s_x, s_y, s_z) = \begin{pmatrix}

s_x & 0 & 0 & 0 \\
0 & s_y & 0 & 0 \\
0 & 0 & s_z & 0 \\
0 & 0 & 0 & 1

\end{pmatrix} \ Translation \Longrightarrow T(t_x, t_y, t_z) = \begin{pmatrix}

1 & 0 & 0 & t_x \\
0 & 1 & 0 & t_y \\
0 & 0 & 1 & t_z \\
0 & 0 & 0 & 1

\end{pmatrix} \ R_x(\Theta)= \begin{pmatrix}

1 & 0 & 0 & 0 \\
0 & \cos\Theta & -\sin\Theta & 0 \\
0 & \sin\Theta & \cos\Theta & 0 \\
0 & 0 & 0 & 1

\end{pmatrix}绕X轴旋转 \ R_y(\Theta) = \begin{pmatrix}

\cos\Theta & 0 & \sin\Theta & 0 \\
0 & 1 & 0 & 0 \\
-\sin\Theta & 0 & \cos\Theta & 0 \\
0 & 0 & 0 & 1

\end{pmatrix}绕Y轴旋转 \ R_z(\Theta) = \begin{pmatrix}

\cos\Theta & -\sin\Theta & 0 & 0 \\
\sin\Theta & \cos\Theta & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1

\end{pmatrix}绕Z轴旋转 \ R_{xyz}(\alpha, \beta, \sigma) = R_x(\alpha)R_y(\beta)R_z(\sigma) $$

旋转时，绕哪个轴旋转，那个轴对应的坐标不变，所以x轴旋转的第一行第一列、y轴旋转的第二行第二列、z轴旋转的第三行第三列

如何证明$R_{xyz}(\alpha, \beta, \sigma) = R_x(\alpha)R_y(\beta)R_z(\sigma)$成立，这个时候需要引入罗德里格斯公式

视图变换 Camera/View

视图就类似使用设计相机拍照，视图就是镜头中的世界

拍一张好照片需要
- 好的地方（Module），搭建场景
- 好的角度（view），视图变换
- 投影（三维空间投影到二维照片）

综上，就是图形学渲染出效果的模型(Model)、视图(View)、投影(Projection)变换，简称MVP变换

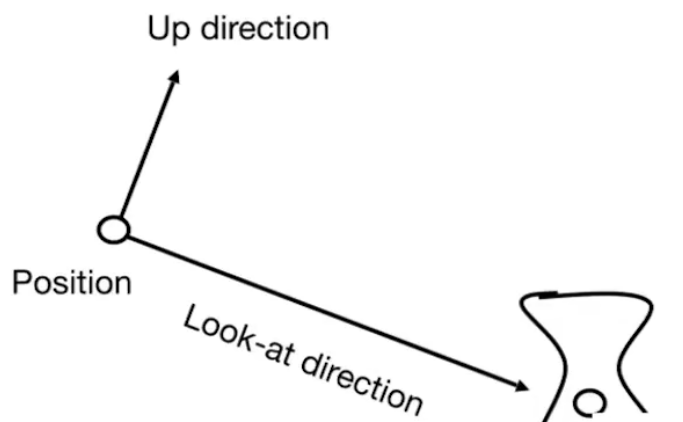
定义相机
- 坐标
- 向上的向量(一个向量就可以确定相机的Roll)
- 朝向

约定：相机永远在原点，永远不动，永远以y轴向上，永远看向-Z轴 其他物体也跟着相机移动

针对坐标为(x, y, z)，角度为(a, b, c)的相机，需要做哪些变换
1. 相机移动到原点坐标
2. 相机的朝向旋转到-Z轴方向
3. 相机的向上向量旋转到Y轴方向

设定相机的朝向向量为g，相机向上的向量为t，可推得相机另一个轴的向量为$g \times t$

$$ T_{view} = \begin{bmatrix}

1 & 0 & 0 & -x_e \\
0 & 1 & 0 & -y_e \\
0 & 0 & 0 & -z_e

\end{bmatrix} 坐标变换矩阵 \ R^{-1}_{view} = \begin{bmatrix}

x_{g \times t} & x_t & x_{-g} & 0 \\
y_{g \times t} & y_t & y_{-g} & 0 \\
z_{g \times t} & z_t & z_{-g} & 0 \\
0 & 0 & 0 & 1

\end{bmatrix} 不加证明给出矩阵R{view}^{-1} \ R{view}^{-1} * \begin{bmatrix}

1 \\ 0 \\ 0

\end{bmatrix} = \begin{bmatrix}

x_{g \times t} \\
y_{g \times t} \\
z_{g \times t} \\

\end{bmatrix} 可见R{view}^{-1}乘以X轴、Y轴、Z轴都等于相机对应的向量坐标 \ R^{-1}{view} * 标准矩阵 = 相机矩阵 \Longrightarrow 相机矩阵 * R{view} = 标准矩阵 \ R{view}^{-1}是R{view}的逆矩阵 \ R{view} = \begin{bmatrix}

x_{g \times t} & y_{g \times t} &z_{g \times t} & 0 \\
x_t & y_t & z_t & 0 \\
x_{-g} & y_{-g} & z_{-g} & 0 \\
0 & 0 & 0 & 1

\end{bmatrix} 不加证明给出矩阵R{view} \ M{view} = R{view} T{view} 组合后得出视图变换矩阵(从右往左的理解顺序，先平移、再旋转) $$

相机和所有的物体都根据该模型移动到特定位置，此时相机肯定是在原点的、看向-Z轴，向上坐标为Y轴的，各个物体的相对位置不变

模型(单独对模型的操作)-视图(对相机的操作并同步到模型上)变换

投影变换

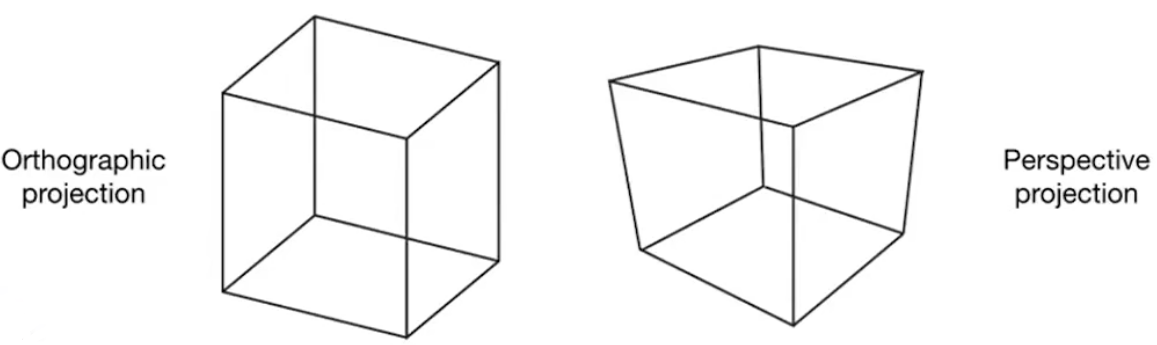
图中左边为正交投影，右边是透视投影

正交投影不会带来近大远小的世界效果，一般用于工程制图
透视投影会有近大远小

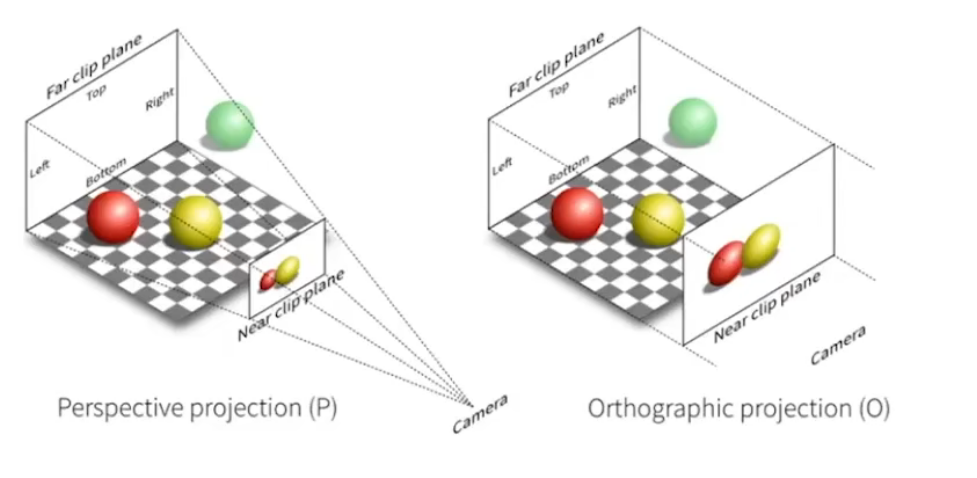
图中左边为透视投影，右边为正交投影

对于正交投影出来的图片结果，可以理解为相机在一个无限远的地方拍照，这样物体之间的距离差距就可以忽略不计了(走路月亮跟着你走的也是这个原因)

正交投影 Orthographic

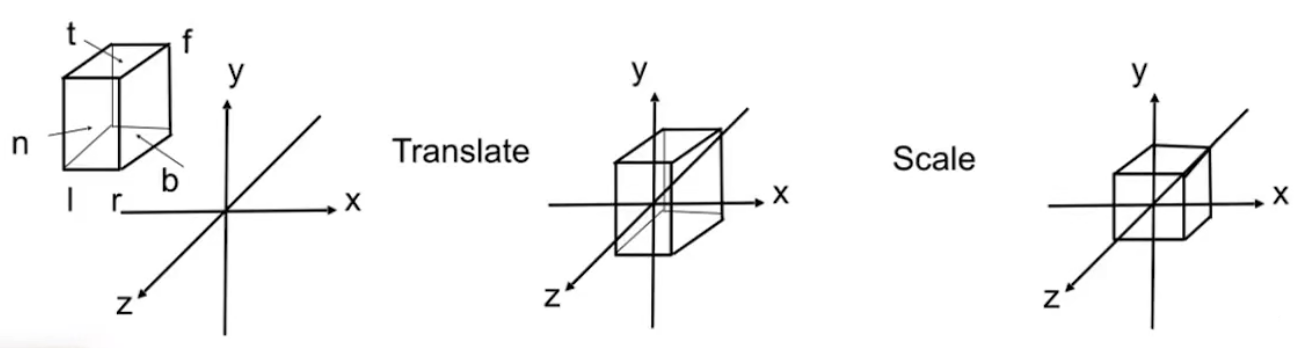
在正交投影中定义一个矩阵，需要定义
- l(left)、r(right)，左平面距离矩形中心的距离和右平面距离矩形中心的距离
- t(top)、b(bottom)，上平面距离矩形中心的距离和下平面距离矩形中心的距离
- f(far)、r(near)，远平面距离矩形中心的距离和近平面距离矩形中心的距离

因为相机朝向是-Z轴，所以f值一般小于r值

在定义完一个矩形之后，需要将其通过一系列变换转换成图片中最右边的标准立方体(canonical cub $[-1 ,1]^3$)

一系列变换指的是
- 矩形移动到原点
- X、Y、Z轴拉伸成[-1, 1]

$$ M_{ortho} = \begin{bmatrix}

\frac{2}{r-l} & 0 & 0 & 0 \\
0 & \frac{2}{t-b} & 0 & 0 \\
0 & 0 & \frac{2}{n-f} & 0 \\
0 & 0 & 0 & 1

\end{bmatrix} \begin{bmatrix}

1 & 0 & 0 & -\frac{r+l}{2} \\
0 & 1 & 0 & -\frac{t+b}{2} \\
0 & 0 & 1 & -\frac{n+f}{2} \\
0 & 0 & 0 & 1

\end{bmatrix} $$

左边缩放矩阵、右边平移矩阵（操作顺序从右往左理解）
暂不考虑旋转

这里对物体做了拉伸，未来还会做一次视口变换，视口变换时会再做一次拉伸

透视投影 Perspective

理论上两条平行的先看起来相交了

前置知识：点(x, y, z, 1)乘以k，得到(kx, ky, kz, k != 0)表示其实也是点(x, y, z, 1)，将k换成z，可以得到(xz, yz, $z^2$,z != 0)，也表示(x, y, z, 1)这个点

(1, 0, 0, 1)与(2, 0, 0, 2)表示同一个点

透视投影分两步
1. 将Frustum平截头体转换成Cuboid矩形
2. 进行一次正交投影
将Frustum平截头体转换成Cuboid矩形
- n(near)平面的四个点不会发生变换
- f(far)平面的z值不会发生变换，只是在平面内进行收缩
- n、f平面的中心点不会发生变化

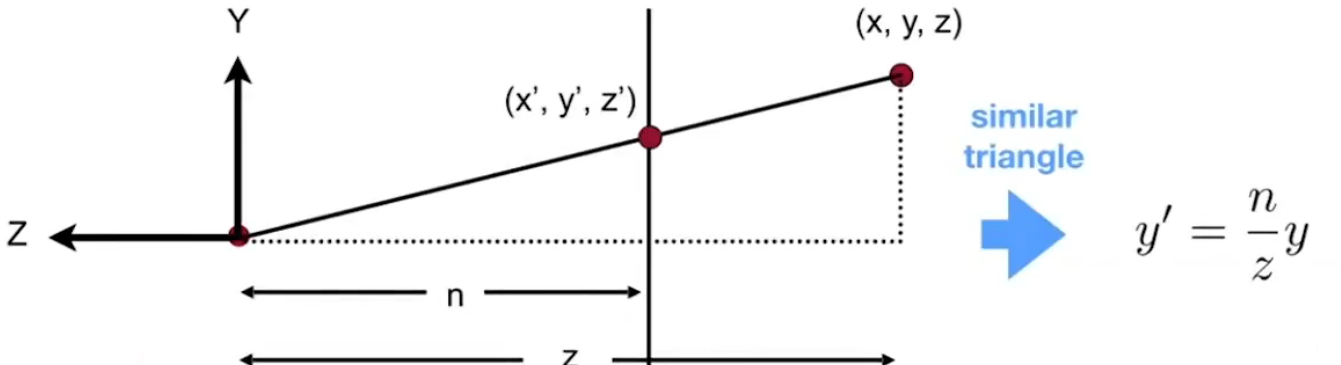
通过侧面观察，更容易得到结论

最左边的红点就是摄像机的位置，中间的红点就是n(near)平面，最右边的红点就是f(far)平面

目标就是将(x, y, z) => (x, y\', z)，通过相似三角形可以推出计算公式

设$M_{persp}$为透视变换矩阵

设$M^{(4\times4)}_{persp \rightarrow ortho}$为透视变换成正交的变换矩阵

得出$M{persp}=M{ortho}M^{(4\times4)}_{persp \rightarrow ortho}$，即将模型先变换成正交可以用的矩形，再通过正交变换矩阵计算

$x=\frac{n}{z}x,y=\frac{n}{z}y$

$$ \begin{pmatrix}

x \\ y \\ z \\ 1

\end{pmatrix} \Rightarrow \begin{pmatrix}

nx/x \\ ny/z \\ unknow \\ 1

\end{pmatrix} == \begin{pmatrix}

nx \\ ny \\ still unknow \\ z

\end{pmatrix} \ M^{(4\times4)}_{persp \rightarrow ortho} \begin{pmatrix}

x \\ y \\ z \\ 1

\end{pmatrix} = \begin{pmatrix}

nx \\ ny \\ unknow \\ z

\end{pmatrix} \Rightarrow M^{(4\times4)}_{persp \rightarrow ortho} = \begin{pmatrix}

n & 0 & 0 & 0 \\
0 & n & 0 & 0 \\
? & ? & ? & ? \\
0 & 0 & 1 & 0

\end{pmatrix} $$

透视变换矩阵最后一行完全可以是(0 0 0 z)，但是z是变量，到时候计算的时候还得实时带入z的真实值，对于计算机来说很麻烦，要开辟内存，还要传值，浪费资源

此时带入观察到的两个细节
- 对近平面来说，(x, y, n, 1) (n表示近平面的z)与透视变换矩阵运算，其x、y、n值不变
- 对远平面来说，(x, y, f, 1) (f表示远平名的z)与透视变换矩阵运算，其f值不变
- 对远平面来说，(0, 0, f, 1) 与透视变换矩阵运算，其值不变，仍未(0, 0, f, 1)

$$ M^{(4\times4)}_{persp \rightarrow ortho} \begin{pmatrix}

x \\ y \\ n \\ 1

\end{pmatrix} = \begin{pmatrix}

x \\ y \\ n \\ 1

\end{pmatrix} == \begin{pmatrix}

nx \\ ny \\ n^2 \\ n

\end{pmatrix} \ 设M^{(4\times4)}_{persp \rightarrow ortho}第三行为 \begin{pmatrix}

A & B & C & D

\end{pmatrix} 带入上述式子的计算中得 \begin{pmatrix}

A & B & C & D

\end{pmatrix} \begin{pmatrix}

x \\ y \\ n \\ 1

\end{pmatrix} = n^2 \ 得到A=0, B=0, C*n + B = n^2 \ M^{(4\times4)}_{persp \rightarrow ortho} \begin{pmatrix}

0 \\ 0 \\ f \\ 1

\end{pmatrix} = \begin{pmatrix}

0 \\ 0 \\ f \\ 1

\end{pmatrix} == \begin{pmatrix}

0 \\ 0 \\ f^2 \\ f

\end{pmatrix} \ 带入前面推理(0, 0, C, D)式子中，得到 Cf + D = f^2 \ \begin{matrix}

Cn + D = n^2 \\
Cf + D = f^2

\end{matrix} \Longrightarrow \begin{matrix}

C = n + f \\
D = -nf

\end{matrix} \ M^{(4\times4)}_{persp \rightarrow ortho} = \begin{pmatrix}

n & 0 & 0 & 0 \\
0 & n & 0 & 0 \\
0 & 0 & n + f & -nf \\
0 & 0 & 1 & 0

\end{pmatrix} $$

将得到的矩阵与（x，y，z，1）相乘后z的值等于(-nf)*z^(-1)+(n+f),是个反比例函数，这个图像恒过（n，n）与（f，f），在n与f之间，z是下凹的，所以z变小了，即再f与n平面之间的点的z是会变小的

光栅化(Rasterization)

将三维空间的几何形体显示到屏幕上
将投影的基本体分解为片段（像素）

通过前面的视图变换、投影变换（正交、透视），我们得到了[-1, 1]^3的标准立方体

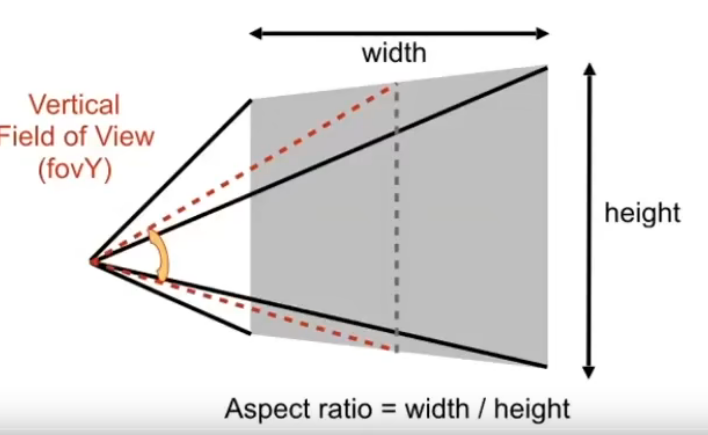
定义视锥需要的两个数据
- 宽高比
- 垂直的可视角度

屏幕：图形学中认为屏幕是一个数组，数组中每一个元素是一个像素
光栅：Raster，就表示屏幕，光栅化(Rasterize)可以理解为把东西绘制在屏幕上
像素：Pixel(Picture Element的缩写)
屏幕空间：在屏幕上定义的坐标系，屏幕左下角为(0, 0)原点，向上为Y轴正方向，向右为X轴正方向
- 坐标从0开始，而不是从1开始
- 屏幕的所有的像素是从(0, 0)到(width - 1, height - 1)
- (x, y)点像素的中心在(x + 0.5, y + 0.5)上
- 屏幕表示的范围从(0, 0)到(width, height)
在不考虑Z轴的情况下，将[-1, 1]的矩阵的x、y坐标映射到屏幕中
- 移动到屏幕中心
- 缩放一下 $$ M_{viewport} = \begin{pmatrix} \frac{width}{2} & 0 & 0 & \frac{width}{2} \ 0 & \frac{height}{2} & 0 & \frac{height}{2} \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1 \end{pmatrix} $$
图形学广泛使用三角形
- 三角形是最基础的多边形
- 任何多边形都可以被拆分成多个三角形
- 三角形三个点肯定在同一个平面
- 三角形内外定义清晰（多边形可能有洞圆环，可能不是凸包）
- 三角形三个点定义不同属性，三角形内部的各个点可以逐渐渐变

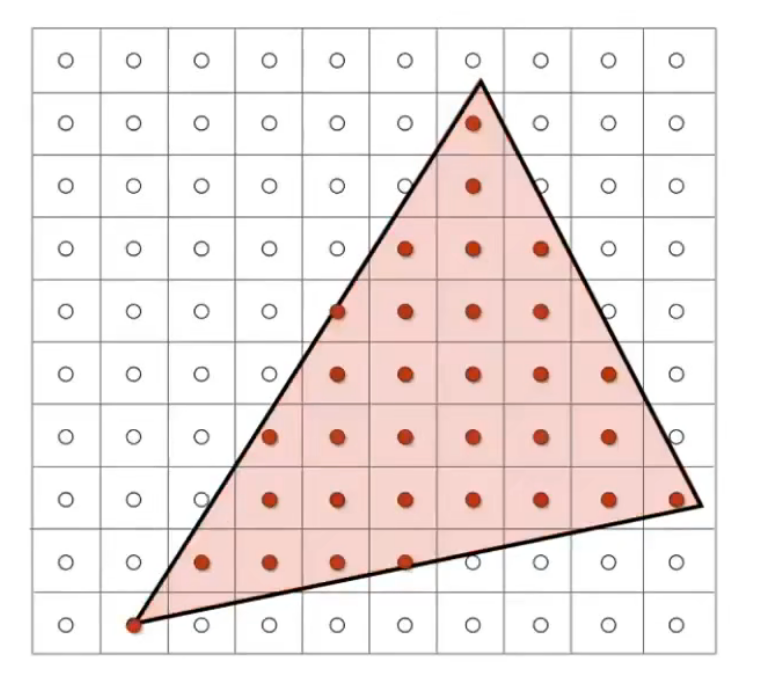
利用像素中心，对屏幕空间进行采样

$$ inside(tri, x, y) = \begin{cases}

1, Point(x, y) 在 tri 这个形状中 \\
0, Point(x, y) 不在 tri 形状中

\end{cases} $$

for(int x = 0; x < width; ++x){
    for(int y = 0; y < height; ++y){
        image[x][y] = inside(tri, x+0.5, y+0.5)
    }
}

通过上述代码就可以知道(x, y)像素是否在多边形中，因为像素中心坐标是(x+0.5, y+0.5)，所以传入的是像素中心坐标

那么如何判断像素点是否在三角形内呢？最开始将的叉乘就可以用到了

判断像素是否在三角形中不用判断(0, 0)到(width, height)中所有的像素，只需要判断三角形三个点中最高、最低、最左、最右所围城的矩阵即可，这个矩阵被称为包围盒

走样与反走样

锯齿、走样、Aliasing

Artifacts表示一切在计算机图形学中的错误(Error)、瑕疵(Mistakes)

锯齿属于一种Artifact，摩尔纹也是一种Artifact，车轮效应也是Artifact

车轮效应就是车轮是顺时针旋转的，但是你看车轮确实逆时针旋转，就是人眼的采样跟不上车轮的旋转导致的

在采样之前做模糊、滤波处理

傅里叶级数展开：任何周期性函数都写成一系列正弦和余弦以及一个常数项的总和

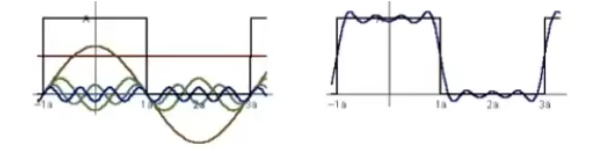
$$ f(x) = \frac{A}{2} + \frac{2A\cos(tw)}{\pi} - \frac{2A\cos(3tw)}{3\pi} + \frac{2A\cos(5tw)}{5\pi} - \frac{2A\cos(7tw)}{7\pi} + ... $$

如上图所示，将很多个不同频率的正弦余弦叠加在一起，拼出一个与目标近似的周期函数，此时运用极限的思想，可以推理出无限个正弦余弦叠加就能拼出目标函数

傅里叶变换：给定任意函数可以通过一系列变换变成另一个函数，还可以把变换后的函数通过逆变换再变回去

傅里叶变换： $F(w) = \int_{-\infty}^{\infty}f(x)e^{-2\pi iwx}dx$
逆傅里叶变换：$f(x) = \int_{-\infty}^{\infty}F(w)e^{2\pi iwx}dw$

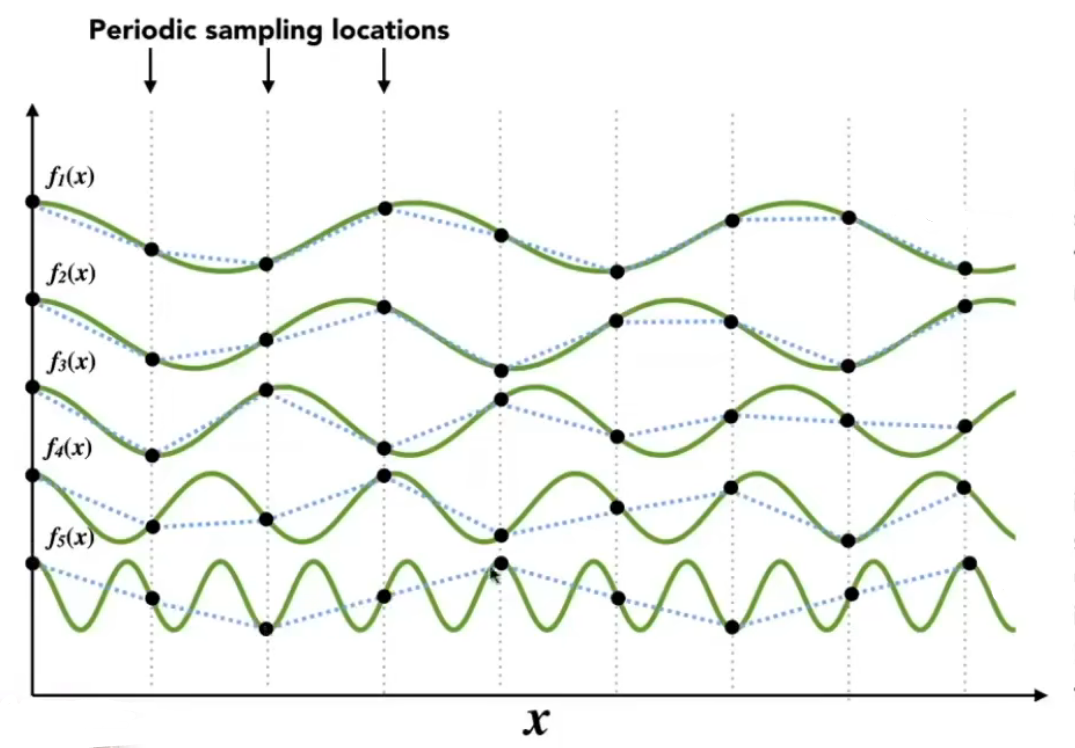
这里给出不同的五种函数从$f_1(x) \Rightarrow f_5(x)$，从上到下频率逐渐增加，我们发现按照虚线对函数进行采样，采样得到的点(途中黑色的点)连起来逐渐不能恢复曲线原来的磨样(黑点之间的链接虚线与原曲线的差距越来越大)

通过上图我们可以发现，当采样的频率跟不上曲线变换的频率的时候，就无法还原出原始信号

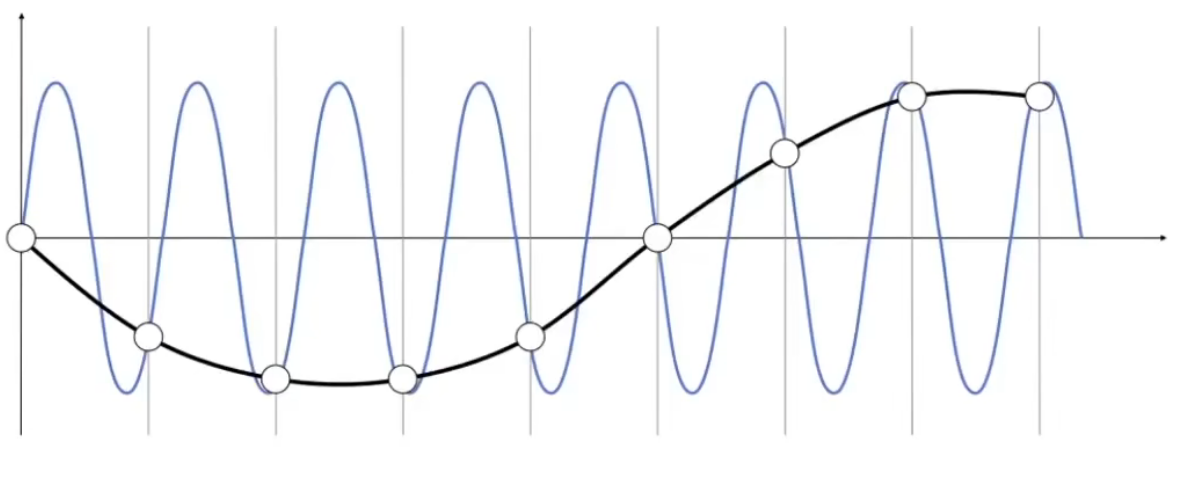
竖线为采样线，白点为采集到的点，蓝色和黑色线表示两种函数

同样的采样方法，采样两种不同的频率的函数，我们无法区分，我们称之为走样

滤波：删除某些特定频率。那么对应的信号应该如何变换

傅里叶变换可以把图片从时域信号变为频域信号

图左为时域信号，图右为频域信号

频域空间图：中心定义为最低频的区域，周围定义成高频区域，不同的频域的地方有多少信息通过亮度来表示

根据上述图片来理解就是：亮点主要集中在中心，说明原图片低频信息多，高频信息少(不是没有)

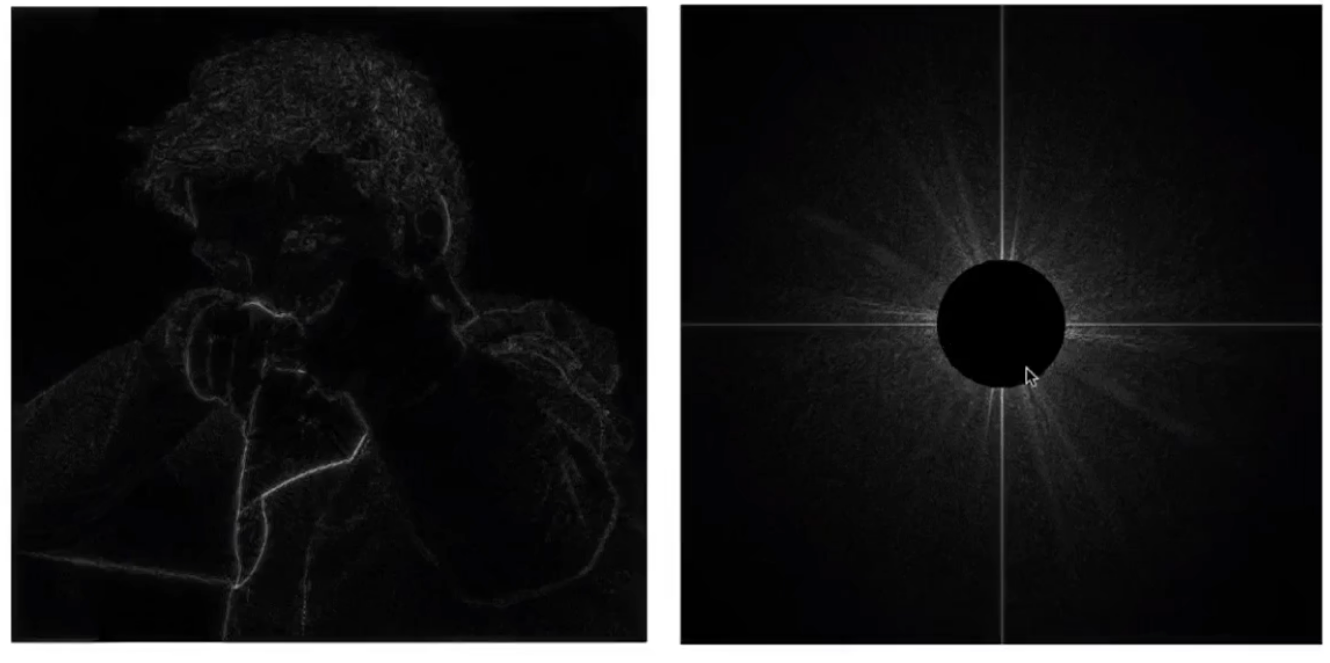
同一张图，如果将频域空间中间的低频信号删除(白色改成黑色)，再逆傅里叶变换回去，可以发现图像的边界特别明显

上述操作就是 高通滤波(把低频的删除，只留下高频)

边界，可以理解成上下或左右差距很大的地方。那么差距大就可以理解为变化频率高，即高频信息，那么通过高频滤波，自然而然就只剩下差距大的地方的了

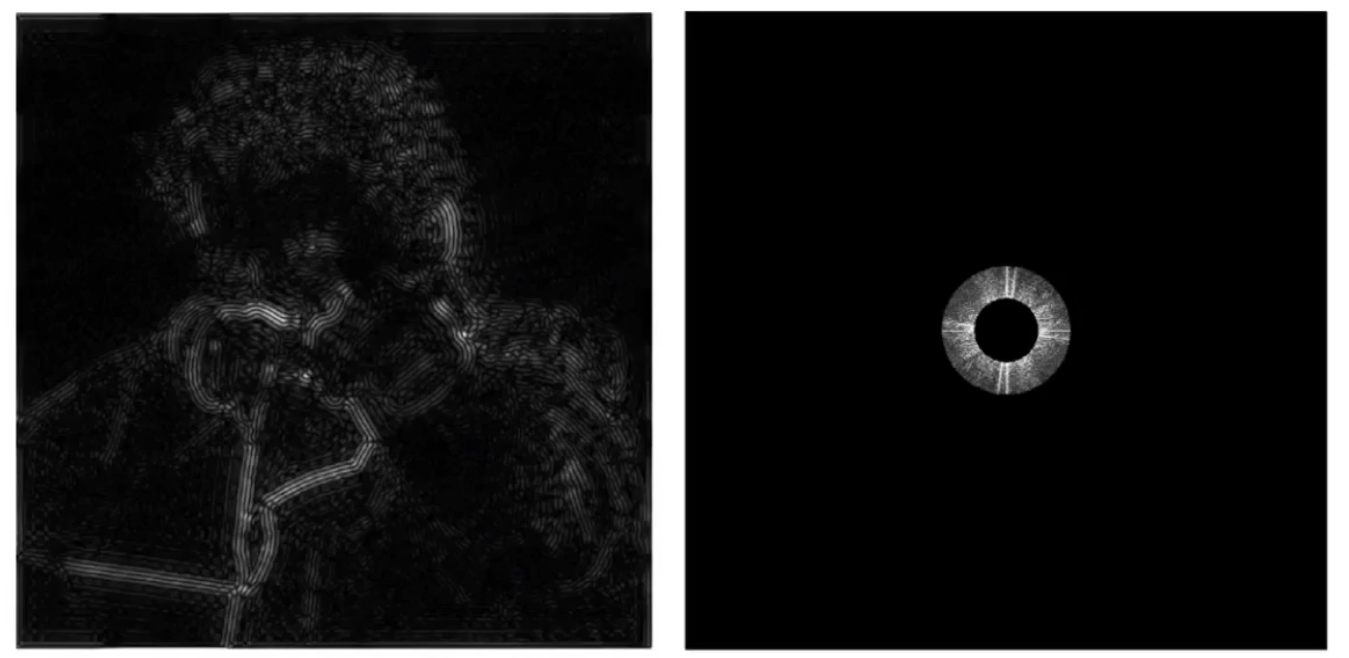
同一张图，如果将频域空间的所有高频信息都删除(除中心点附近特定半径内，都设为黑色)，再傅里叶变换回去，可以得到一张很模糊的图片

上述操作就是低通滤波(低频率通过高频率去掉)

特定内容在，数字图像处理中学习

滤波

滤波 = 去掉特定频率的信息 = 平均 = 卷积

Filtering = Convolution = Averaging

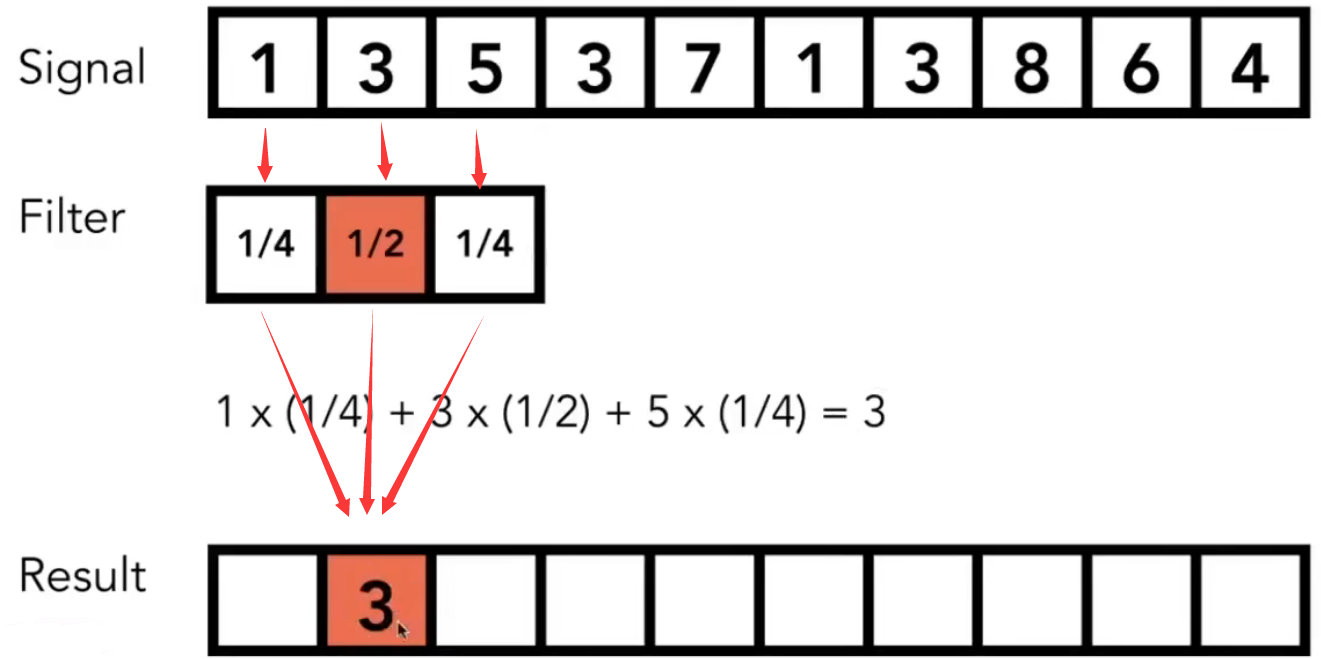
简单卷积的理解
Filter：滤波器、Siganl：信号

在移动Filter窗口的过程中，将Signal的三个数和Filter的三个数做一个点乘，再将计算结果写回窗口的中心值(说白了就是一种加权平均)

也就是说，卷积作用在一个信号上，用某种滤波器对信号进行卷积操作，并且得到一个结果

并不是真实数学上的定义，仅仅是图形学上的简化定义

卷积的定理
- 时域上如果对两个信号进行卷积，对应两个信号各自的频域上，两个信号频域的乘积
- 时域上如果是乘积，那么频域上就是卷积

可以拿到一个图，用某种滤波器去做卷积操作
也可以得到图片的傅里叶变换的频域，再把卷积的滤波器变换到频域上，再把两者相乘，得到的频域的结果，最后将结果逆傅里叶变化到时域上

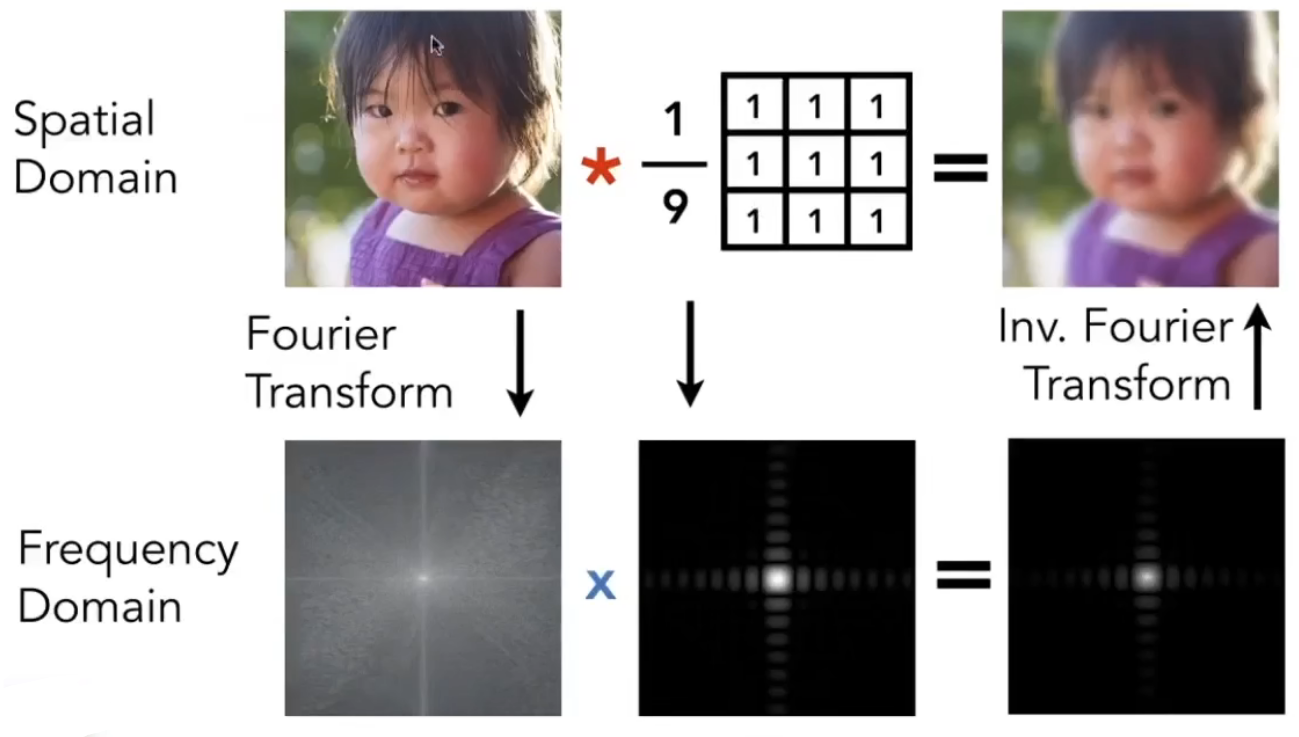
均值滤波

上面图片可以分上下两块理解
- 对图片的每个像素都等于自己和周围8个像素的平均值(对时域图做卷积操作)
- 对傅里叶变化的频域与滤波器的频域相乘(对频域图的乘法操作)

可以发现上述两种操作，得到的结果是相同的

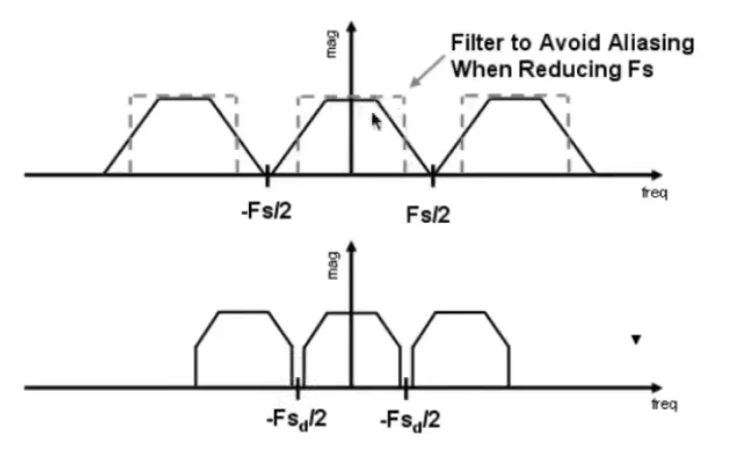
采样

Sampling = Repeating Frequency Contents

采样就是重复频域上的内容

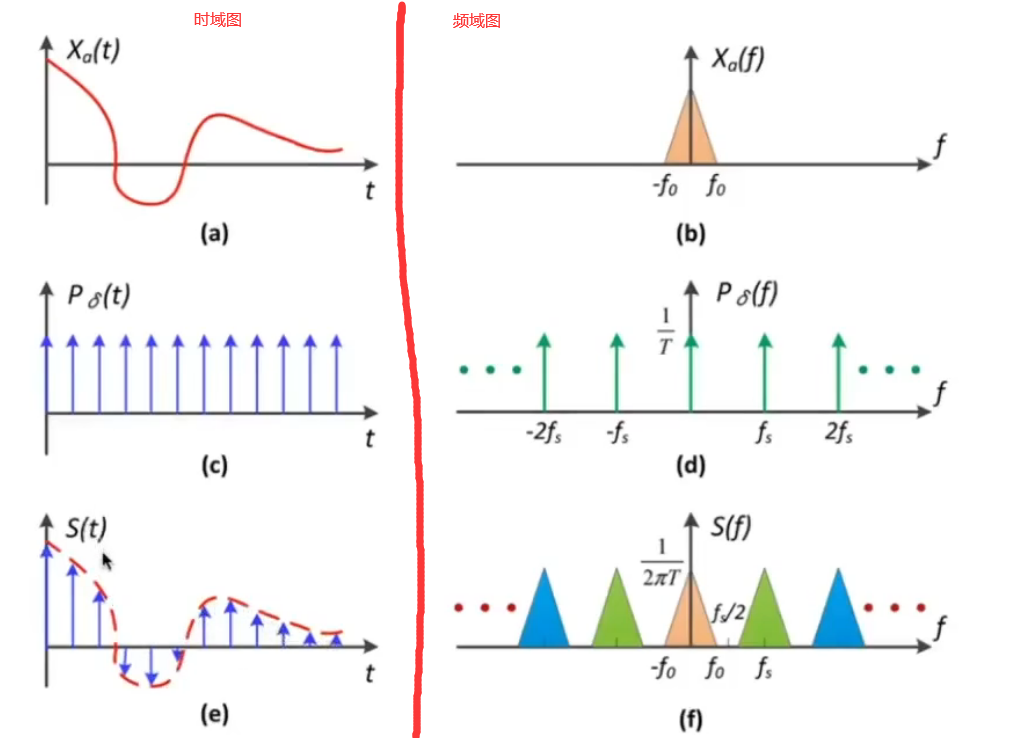
图(a) : $X_a(t)$为原函数图像
图(c) : $P_\delta(t)$为冲击函数
图(e) : $S(t)$为原函数与冲击函数乘积的结果，就是$X_a(t)$函数上离散的点
图(b) : $X_a(t)$函数傅里叶变换之后的函数
图(d) : $P_\delta(t)$冲击函数傅里叶变换之后的新的冲击函数
图(f) : 图(b)与图(d)的卷积的结果

图(c)的冲击函数，就是只有在竖线上才有值，也就是说图(a)与图(c)的乘积就是在图(a)上周期行的取一些点，就跟之前的取样一样的

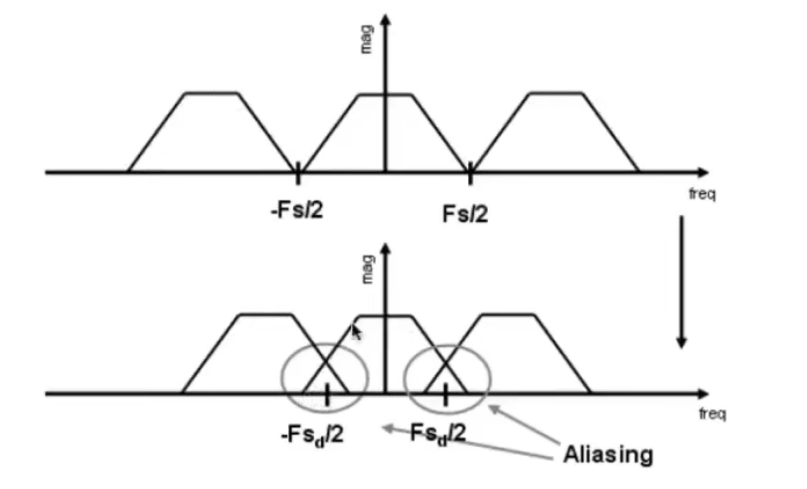
采样：在频率上的理解就是重复一个原始信号的平铺

上图中，上面是合理的采样周期，原始信号的平铺是井然有序、严丝合缝的；当采样率不足或采样不够快，就会导致原始信号的间距越小

那么，我们可以称在频域中，频域的平铺在搬移的情况下发生了混合(混叠)，就是产生走样的原因

时域中采样越稀疏，在会让频域中的原始数据越密集

反走样

增加采样率(减少频域上平铺的混合)，增加屏幕分别率

对于同一台设备，不具有实用性，并不能要求使用者更换显示器

先做模糊，再做采样

通过低通滤波，去掉高频信息，再采样

通过去掉高频信号，让原本混叠的部分，不再混叠，从而减少了走样

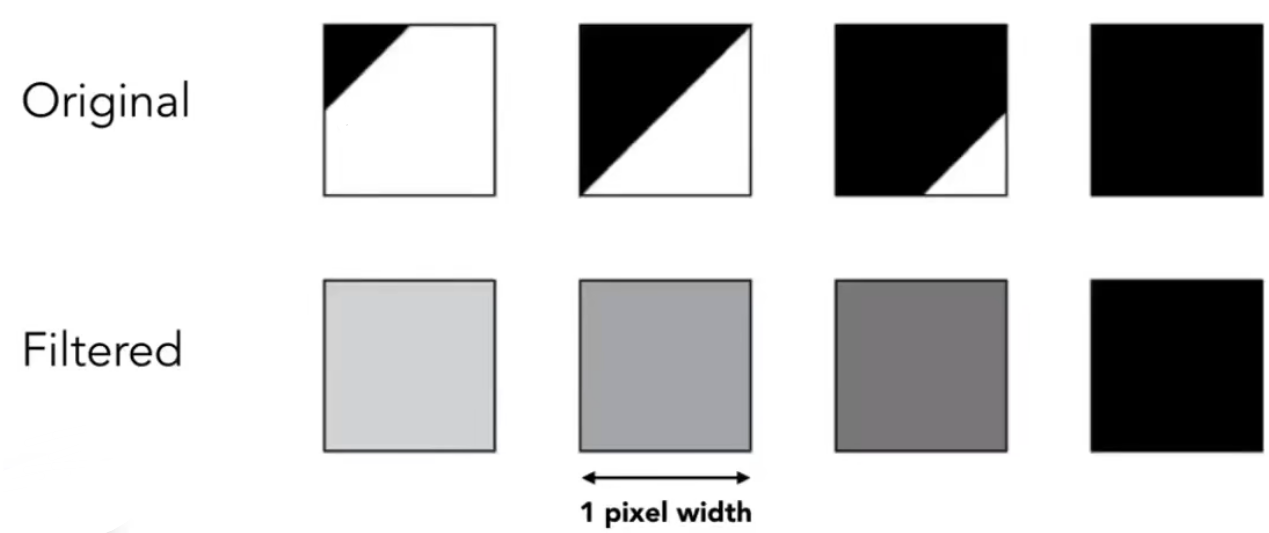
如何模糊：使用一定大小的低通滤波器对每个像素的覆盖面积做一个卷积

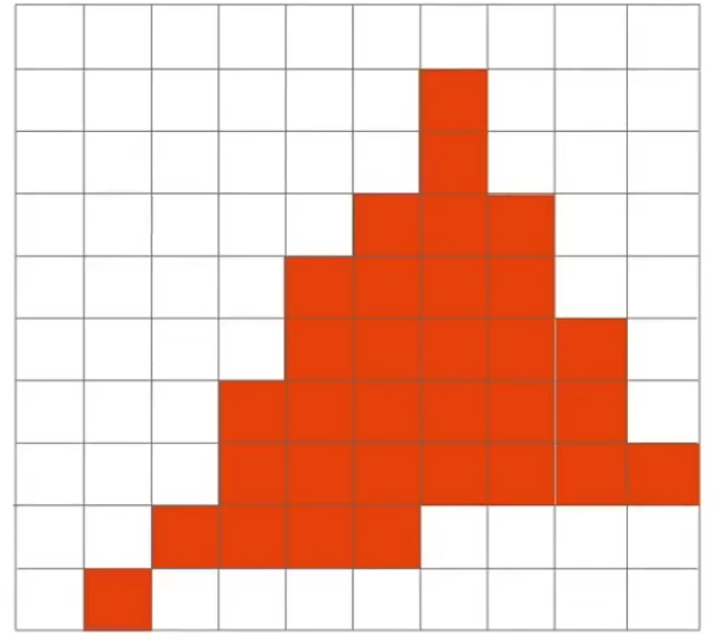
Original是每个像素可能出现的情况，被覆盖小部分、被覆盖一半、被覆盖大部分、被完全覆盖

Fileterd是每个像素通过低通滤波器卷积后的结果

那么如何计算三角形在每个像素中占的比例多少呢？不容易、计算量大

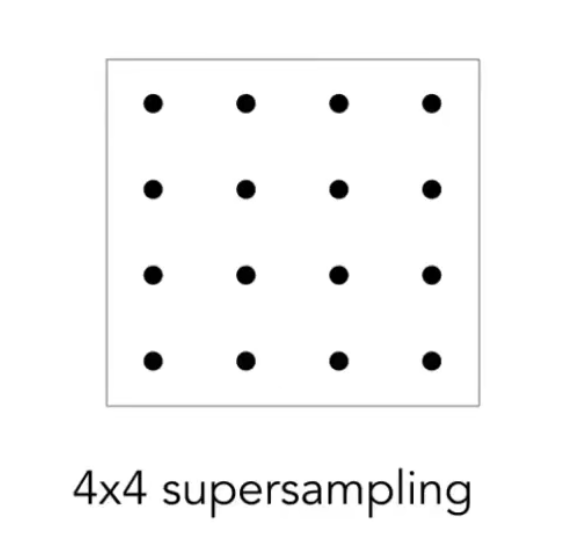
Antialiasing By Supersampling(MSAA)多重采样抗锯齿

这是近似算法，严格意义上不能解决走样问题

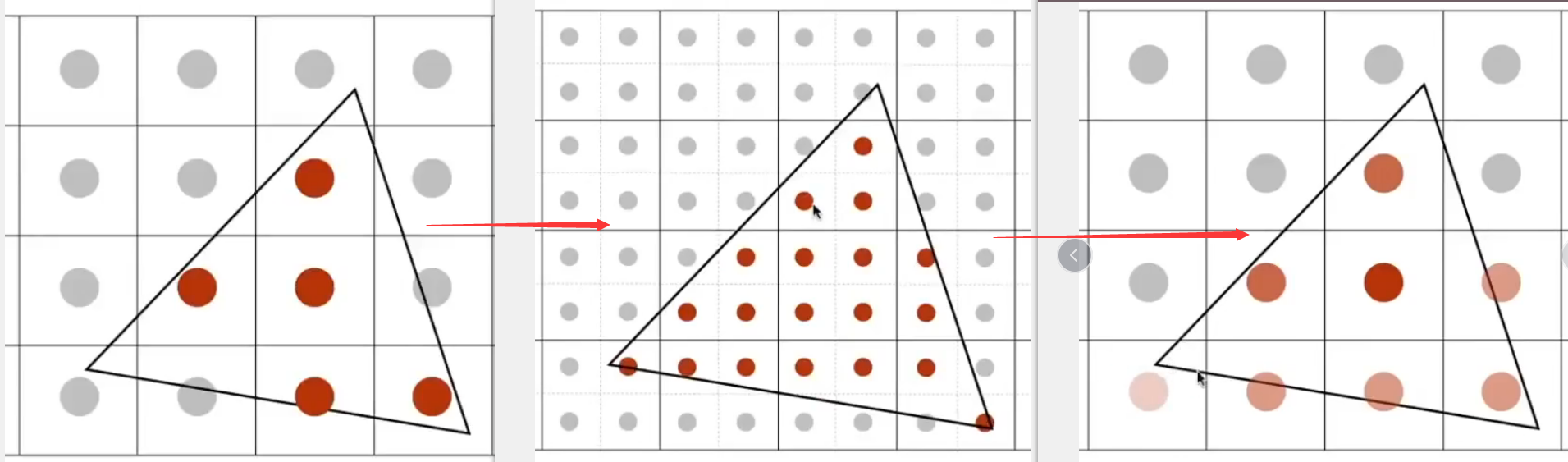
将一个像素，分成若干个小的像素(图中是将一个像素分成4*4，黑色的点表示各个小像素的中心点)，然后再判断各个小像素的中心点是否在三角形中，再把判断结果平均一下，就能得到当前像素百分之多少在三角形中的近似值

MSAA解决的对信号的模糊操作，只不过MSAA最后的出来的值也可以用作采样

为了使用MSAA：增加了计算量(每个像素内又多算了很多次)：工业上会通过更加有效的图案来分布不同的点，而不是这里的均匀分布；也有计算结果复用

FXAA(Fast Approximate AA)

快速近似抗锯齿

TAA(Temporal AA)

通过上一帧的信息，感知到的信息，来推测

Super Resolution / super sampling

超分辨率/超采样

将512*512的图片拉伸成1024*1024的图片时，会出现非常明显的锯齿

解决方法就是DLSS(Deep Learning Super Sampling)，就是通过深度学习去猜测缺失部分的信息内容，并且补足

深度缓冲

很多三角形叠在一起的时候，怎么处理？

要让离摄像机近的物体遮挡远处物体，通过深度缓冲，也叫Z-Buffer

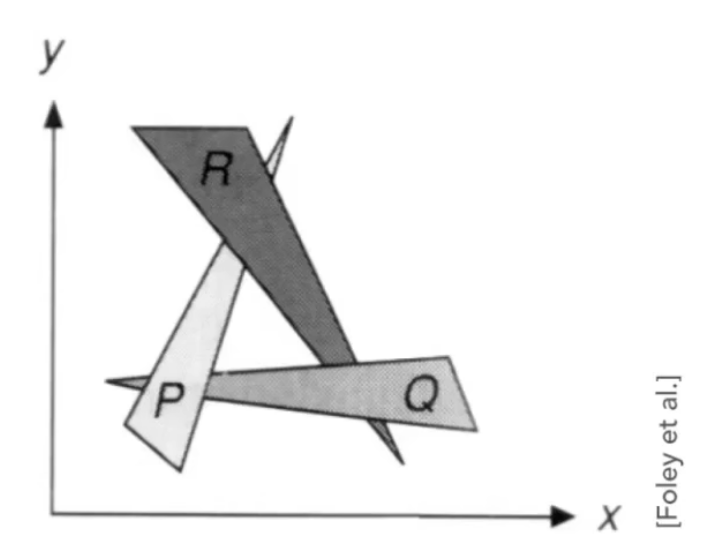
画家算法

先画远处的面，再画近处的面，一层一层的覆盖

需要先对所有的三角形面片进行排序，时间复杂度 $O(n\log _2n)$

画家算法无法解决这种互相遮挡的关系

Z-Buffer

对单独的三角形面片无法排序，那么直接对单个像素进行处理，保证单个像素所存的是其看到的几何物体的最浅的深度信息，即深度图，深度缓存

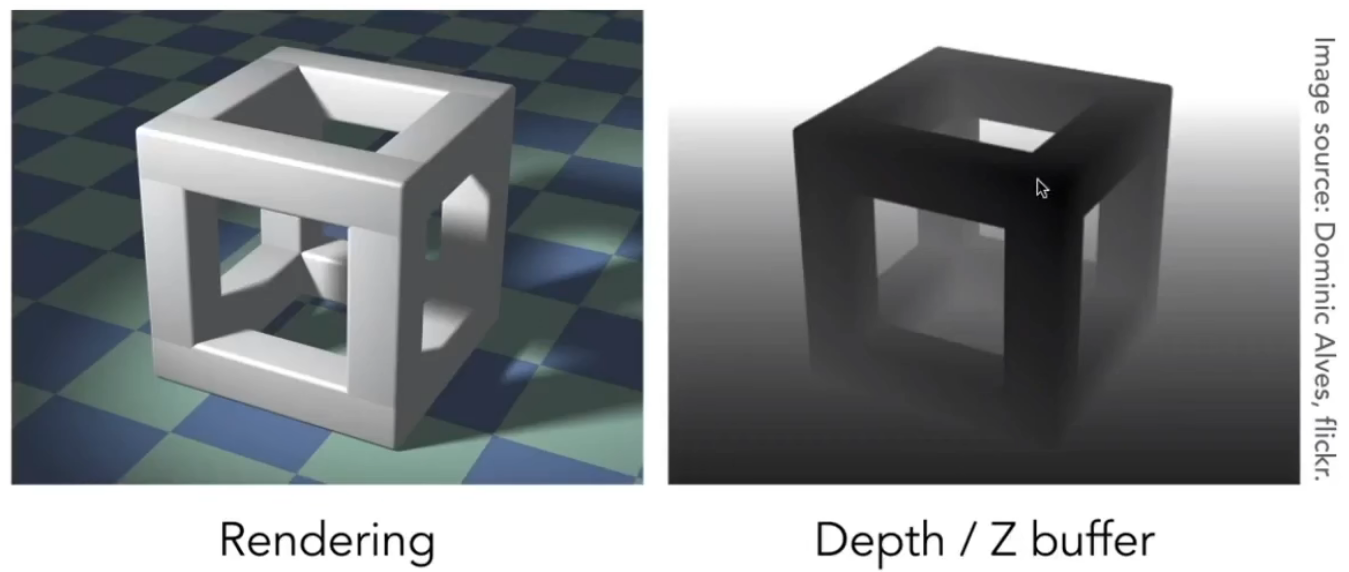
左边为渲染出的图片，右边为深度图

深度图中，越近越黑，越远越白

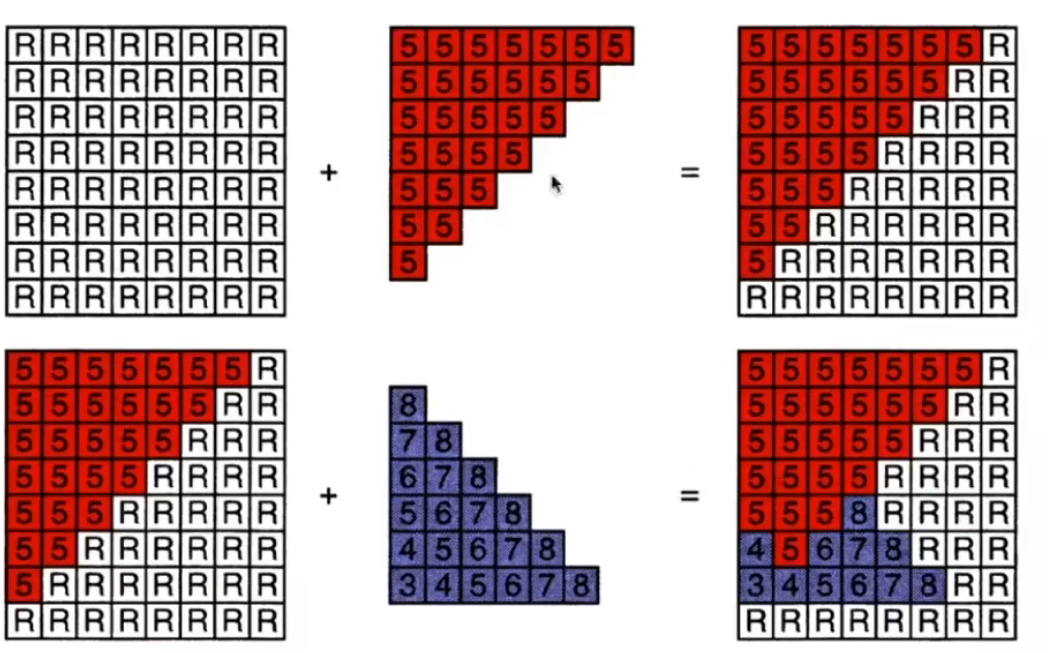
图中每个格子表示一个像素，先来了个一个三角形深度都是5，R表示无限大，则5比无限大小，可以覆盖；然后来了个新的三角形，根据深度信息进行覆盖操作

一般而言，n个三角形，每个三角形覆盖常数个像素，那么最终时间复杂度只是$O(n)$

着色

shading，引入物体的明暗的不同，颜色的不同，对不同的物体应用不同的材质的过程

Blinn-Phong反射模型

反射
- 高光
- 漫反射
- 间接光照

定义
- 在局部，比较小的范围内，物体表面是一个平面(无论物体长什么样)
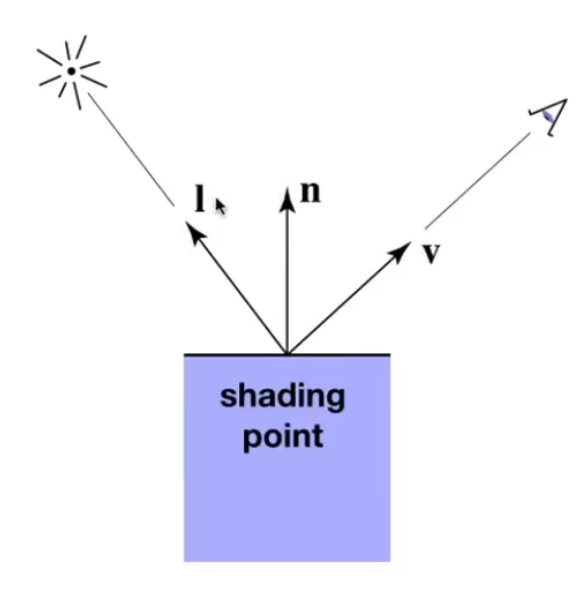
- 定义垂直于平面的法线n
- 摄像机的观察方向v
- 看向光源的方向l
- 颜色color
- 光的亮度 shininess

所有的方向都是单位向量，只表示方向

漫反射

暂且只讨论某一个点的着色，也就是只考虑光照的方向，而不考虑照向这个点的光是不是被挡住了

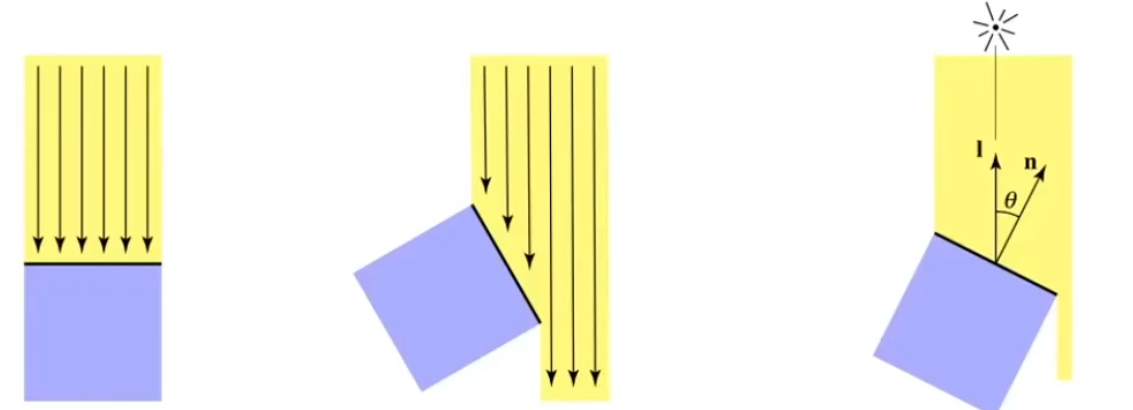
同一束光照，当紫色物体旋转时，其单位面积接收到的光变少，导致其变暗

任何一个着色点周围单位面积能接受到多少光照，与光线的角度成一定关系，从而引出Lambert's定律：接受到的光照与l和n的余弦(上图中的 $\cos \theta$)成正比

带入现实，一个是太阳能板，被照射面积越大热得越快；一个是四季，夏天是被太阳光直射

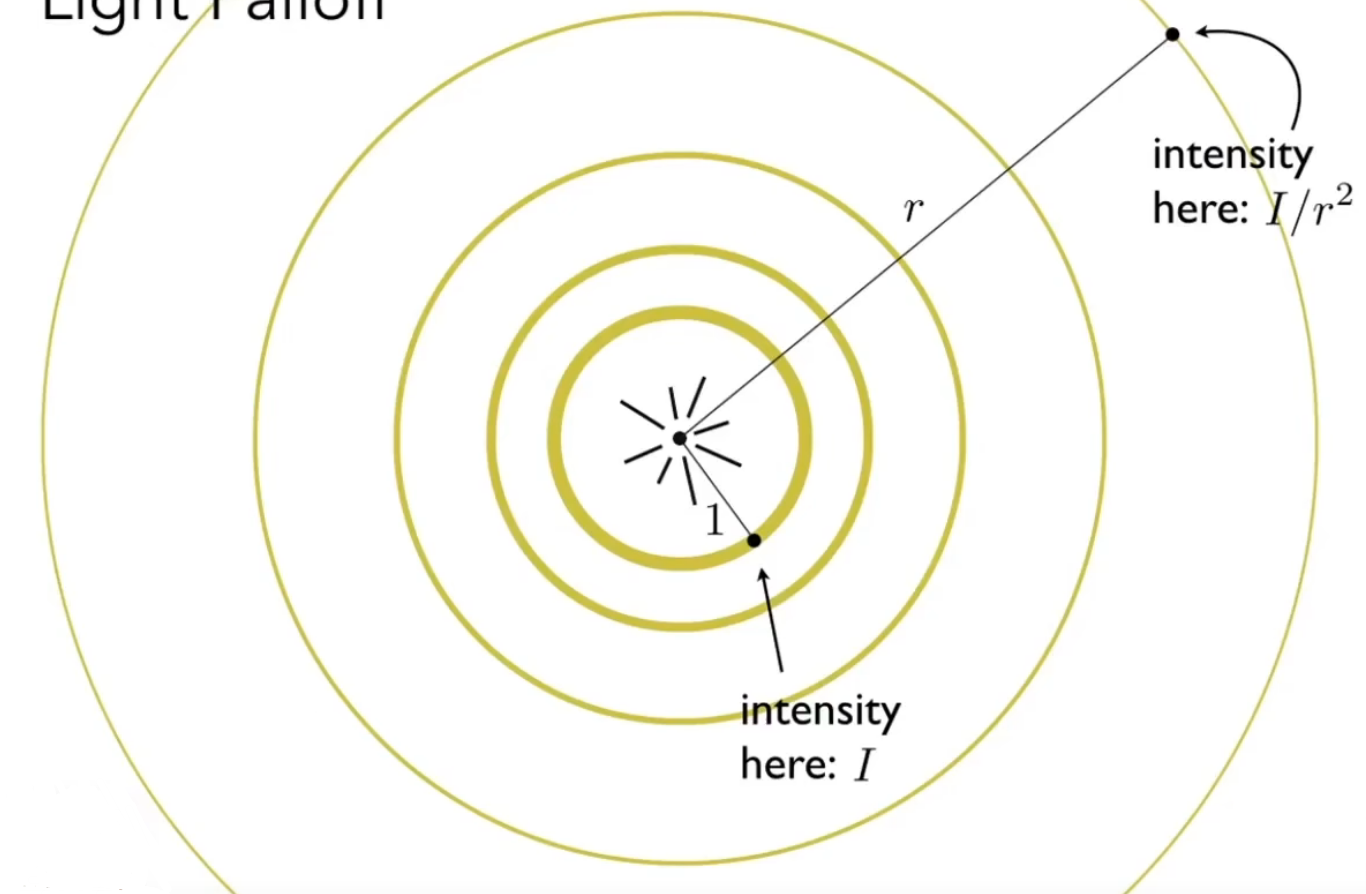
对于一个光源，某一瞬间，其发出的能量是固定的，而伴随着光线的传递，其蕴含的能量也逐渐分散(球壳，而不是圆形)

此时定义距离为1是，光线强度为I，当距离为r，则光纤强度为 $\frac{I}{r^2}$，通过这个式子可以算出当前传播到着色点的光照强度

通过上面两个公式，可以得到着色点(Shading Point)的光照强度、多少光会打在着色点上，得到计算式子

$$ L_d = k_d(I/r^2)max(0, n \cdot l) $$

上面的数学表达式就是漫反射的表示方法
- $k_d$漫反射的系数，表示这个点吸收多少能量(类似物体吸收所有颜色就是黑色，不吸收所有颜色就是白色的物理规律)
- $I/r^2$ 到达着色点的能量
- $max(0, n \cdot l)$ 接收了多少能量

为什么是$max(0, n \cdot l)$ ，$n \cdot l$也就是$\cos \theta$可能为负数，因为光线可能从物体下面往上发射，而这种光不具备物理意义（这里只讨论发射，不讨论折射）

漫反射的物理规律就是看一个物体无论从什么角度看都是一样的，而上面的$L_d$式子刚好与观察方向v没有任何关系

通过前面的解释，可以清楚的了解为什么这个球是渐变的，从亮变灰再变黑

通过定义$k_d$颜色系数，可以定义该物体整体上的明暗

几何

如何表示光滑的曲线、曲面、将简单曲面通过细分的方法得到复杂曲面、形状发生变化时面如何变化、如何保持物体的拓扑结构…

图形学.md 34 KB

História Raw

前提知识

线性代数

点乘

叉乘

矩阵

变换

仿射变换

伸缩变换(Scale)

镜像

切变

旋转(Rotate)

平移(Transiation)

总和

逆变换

组合变换

变换的分解

三位空间的变换

视图变换 Camera/View

投影变换

正交投影 Orthographic

透视投影 Perspective

光栅化(Rasterization)

走样与反走样

滤波

采样

反走样

增加采样率(减少频域上平铺的混合)，增加屏幕分别率

先做模糊，再做采样

Antialiasing By Supersampling(MSAA)多重采样抗锯齿

FXAA(Fast Approximate AA)

TAA(Temporal AA)

Super Resolution / super sampling

深度缓冲

着色

Blinn-Phong反射模型

漫反射

几何

光线追踪（Ray Tracing）

动画模拟、仿真

图形学.md 34 KB História Raw

前提知识

线性代数

点乘

叉乘

矩阵

变换

仿射变换

伸缩变换(Scale)

镜像

切变

旋转(Rotate)

平移(Transiation)

总和

逆变换

组合变换

变换的分解

三位空间的变换

视图变换 Camera/View

投影变换

正交投影 Orthographic

透视投影 Perspective

光栅化(Rasterization)

走样与反走样

滤波

采样

反走样

增加采样率(减少频域上平铺的混合)，增加屏幕分别率

先做模糊，再做采样

Antialiasing By Supersampling(MSAA)多重采样抗锯齿

FXAA(Fast Approximate AA)

TAA(Temporal AA)

Super Resolution / super sampling

深度缓冲

着色

Blinn-Phong反射模型

漫反射

几何

光线追踪（Ray Tracing）

动画模拟、仿真

图形学.md 34 KB

História Raw