|
|
1 ano atrás | |
|---|---|---|
| .. | ||
| Image | 1 ano atrás | |
| Path_Planning_for_Autonomous_Mobile_Robots_A_Revie.pdf | 1 ano atrás | |
| README.md | 1 ano atrás | |
README.md
Recast Navmesh
推荐文章
- 知乎
Recast Navigation源码解析:https://zhuanlan.zhihu.com/p/484520809 - 知乎
Recast Navigation基础:https://zhuanlan.zhihu.com/p/74537236 Recast Tutorial:https://digestingduck.blogspot.com/2010/02/slides-from-past.html
重要论文
- Path Planning for a vision-based autonomous robot
- Simplified 3D Movement and Pathingfinding Using Navigation Meshes
- Volumetric cell-and-portal generation
- Crowdws In A Polygon Soup: Next-Gen Path Planning (GDC, 推荐)
导论
根据时间顺序,有这么几个重要概念被提出
| 里程碑 | 作者 | 时间 |
|---|---|---|
| Meadow Mapping | Ronald C. Arkin | 1986 |
| Volumetric Cell-and-protal generation | Denis Haumont | 2003 |
| Corwds In A Polygon Soup: Next-Gen Path Planning | David Miles | 2006 |
| Recast Navigation | Mikko Mononen | 2008 |
Meadow Mapping
Ronald C. Arkin 是一位美国计算机科学家,他在 1987 年发表了一篇论文 《Path planning for a vision-based autonomous robot》 ,介绍了 Meadow mapping 的原理和实现
Meadow mapping 是一种用于生成导航网格的方法,它将自由空间分解成凸多边形的集合,然后以每个凸多边形的边缘中点作为寻路节点,使用 A* 算法进行寻路。它还可以根据不同的地形类型(如人行道,草地,砾石等)设置不同的代价函数,优化寻路结果。它是现代 Navmesh 系统的雏形。
Path planning for a vision-based autonomous robot 论文)
Meadow Mapping 提出一个概念:把世界凸多边形化
为什么是凸多边形?
- 凸多边形内任意俩点连接不会超出多边形区域
- 凸多边形边上的点便于做寻路最小单位
凸多边形内部不需要寻路
我们只需要将世界划分成多个凸多边形,那么就只需要研究凸多边形之间如何连通即可,凸多边形内部直接一根直线连接即可
于是我们将寻路问题转换为以凸多边形边缘中心为节点的图论搜索问题
为什么不用 Grid (网格) ?
对于大面积的开放区域来说,格子作为寻路基本单位则数量庞大;但是一个凸多边形可以是一个很大的区域,所以对于寻路来凸多边形的效率更高
所以一个寻路流程大概如下
- 得到一个 3D 场景
- 获得可行走区域
Reachable Space(以前是手动绘制,现在可以自动绘制) - 将可行走区域划分成多个凸多边形
Convexify the Space - 凸多边形为单位,继续路径查询
Path Finding - 路径改进,得到更为平滑的路径
那么会有这么几个问题?
- 如何自动绘制可行走区域
- 如何区域划分凸多边形
- 如何进行路径查询
区域划分凸多边形
如果区域是凸多边形,则直接结束算法
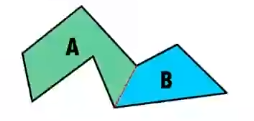
如果区域不是凸多边形,则找到一个凹的角(>180°),尝试将其与多边形内部其他的点连接起来,这个时候会得到两个新的区域,也就是上图的 A 和 B,然后对这两个区域再进行相同的算法,如此一来整个场景就都是凸多边形
也就是递归的二分法
- 如何判断一个多边形是凸多边形?
检查是否存在大于 180° 的角
规定凸多边形节点顺序按照逆时针走
向量 (x-, x) 和向量 (x, x+) 进行叉乘,可以判断点 x+ 在向量 (x-, x) 的左边还是右边。叉乘的结果如果是正数那么就是在左边,反之在右边
以上图为例,点 x+ 在向量 (x-, x) 的右边,那么这个点的角度大于 180°
以上图为例,点 x+ 在向量 (x-, x) 的左边,那么这个点的角度小于180°
通过上面的发现,我们只需要遍历凸多边形所有的点,即可判断每个点的角度是否大于180°,以此判断该多边形是否是凸多边形
- 如何将大于 180° 角的点连接到多边形其他可见顶点上?
检查所有多边形节点与之连线是否为对角线
- 对角线的要求
- 条件1:不与多边形的边相交
- 条件2:在多边形内部
上图中 af 与 gh 相交,不符合条件1 上图中 ag 不在多边形内部,不符合条件2
以凹点 a 为例,对 a 点来说 g、f 两点就是不可见的,因为 ag 连线完全在多边形外,af 连线与 gh 连线相交
这里推荐一本书 《Computational Geometry in C》
如何判断 af 和 gh 线段相交?
高中数学提供的解决方案就是点斜式求斜率,然后进行计算。但是在计算机中,直接根据 k = (y2 - y1) / (x2 - x1) 算出来使用 double 存储可能存在精度问题,或者除 0 错误
这里依然使用叉乘的思想
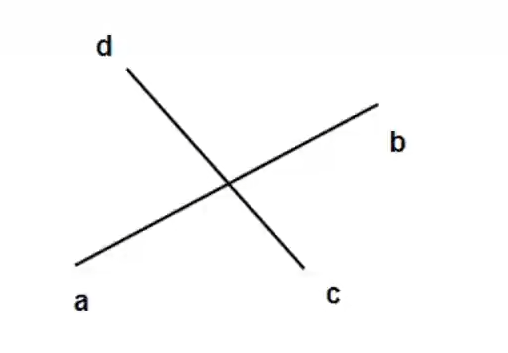
如果 a、b 两点在 dc 线段的两端,并且 d、c 两点在 ab 线段的两端,那么线段 ab 和 dc 相交
bool isCross(Vector2D a, Vector2D b, Vector2D c, Vector2D d) {
// c、d 两点在线段 ab 的两端
bool cd_cross = isLeft(a, b, c) ^ isLeft(a, b, d);
// a、b 两点在线段 cd 的两端
bool ab_cross = isLeft(c, d, a) ^ isLeft(c, d, b);
return cd_cross && ab_cross;
}
上述代码使用异或来判断是否满足两点在线段两端的判断,如果两点都在右边或者都在左边,那么异或的结果就是 false,如果两点一个在左边一个在右边则异或的结果是 true
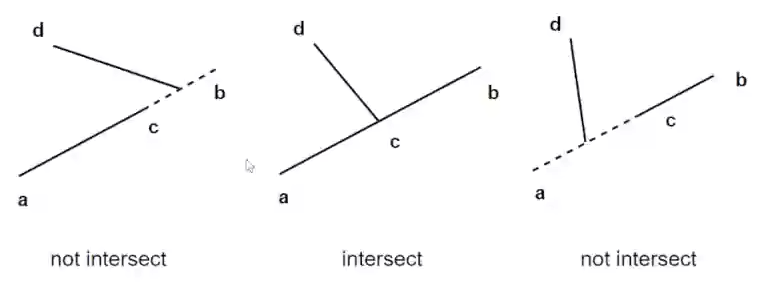
但是上述解法无法处理共线问题,比如上图所示,点 c 在线段 ab 上,所以需要额外判断共线问题
所以判断线段是否相交的大概算法如下
bool isCross(Vector2D a, Vector2D b, Vector2D c, Vector2D d) {
if (c 与 ab 共线) {
return c 是否在线段 ab 上;
}
if (d 与 ab 共线) {
return d 是否在线段 ab 上;
}
if (a 与 cd 共线) {
return a 是否在线段 cd 上;
}
if (b 与 cd 共线) {
return b 是否在线段 cd 上;
}
// c、d 两点在线段 ab 的两端
bool cd_cross = isLeft(a, b, c) ^ isLeft(a, b, d);
// a、b 两点在线段 cd 的两端
bool ab_cross = isLeft(c, d, a) ^ isLeft(c, d, b);
return cd_cross && ab_cross;
}
判断 c 是否与 ab 共线,可以通过 c 到直线 ab 的距离来判断,小于一个极小值就算共线
判断 c 是否在线段 ab 上则直接通过坐标计算即可
通过上面判断线段相交可以处理处理线段 af 与 gh 的情况,那么如何处理 ag 线段在多边形外的情况呢?
我们先定义什么是锥形
以上图为例,直线 (x, x-) 和 直线 (x, x+) 就可以构成一个锥形
我们先分类讨论,如果是凸点(小于 180° 角的点),那么对角线在锥形范围内;如果是凹点(大于 180° 角的点),那么对角线在锥形范围外
所以算法的重点在如何判断直线在锥形范围内
其实也很简单,如果点在锥形范围内,那么该点在 (x-, x) 线段左边,并且在 (x, x+) 线段左边
综合以上几种算法,我们可以检测对角线是否与非临边相交和对角线是否在锥形内部
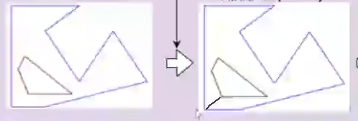
如果多边形内部存在 hole (洞),解决方法其实也很简单,将内部洞与外围点连接,将带空洞的多边形变为简单多边形,当然这个内部洞与外围的连接点也必须是互相可见的
上图连接的一根线,将带空洞的多边形变成了下图这种简单多边形,下图稍微夸张了一点分割部分,主要是为了强调这根线的作用
在 Recast Navigation 中,划分凸多边形使用的是耳切法(Ear Clipping),Meadow Mapping 划分凸多边形则使用的是二分法。耳切法使用更加聪明的方式,使得每个切出来的区域都是单独的三角形,避免 Meadow Mapping 递归调用的额外开销
Recast Navigation 是一种基于耳切法的划分算法,它的基本思想是从一个凸多边形的任意一个顶点开始,判断该顶点是否是一个耳朵,即该顶点的内角小于 180°,并且以该顶点为顶点的三角形不包含其他顶点。如果是耳朵,那么就将该顶点和相邻的两个顶点组成一个三角形,从多边形中切除该耳朵,否则就跳过该顶点,继续检查下一个顶点。重复上述过程,直到多边形被切割成若干个三角形为止。然后对每个三角形进行合并,使其满足最大顶点数的限制,得到最终的凸多边形集合。这种算法的优点是划分后的多边形的角度较大,有利于寻路效率,缺点是划分后的多边形数量较多,占用空间较大
寻路优化
Meadow Mapping 采用 A* 算法进行寻路
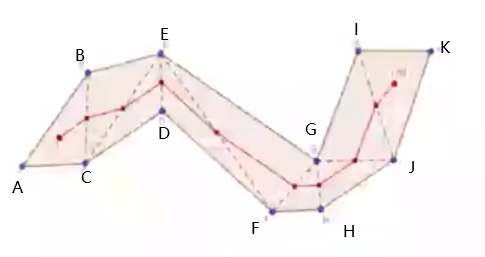
很明显上面的路径并不是真实意义上的最短路径,以 DE 线段上的路径点为例,如果路径点在D上明显可以缩短路径
所以 Meadow Mapping 提出了一个路径改善算法,采用局部贪心的策略:遍历每个在边检中点的路径节点,考虑三种方案
- 保持路径在边界中点不变
- 选择边界左边节点
- 选择边界右边节点
针对以上三种方案,选择距离最短的路径
Recast Navigation在路径优化时使用String pulling漏斗算法