|
|
před 4 měsíci | |
|---|---|---|
| .. | ||
| Image | před 4 měsíci | |
| src | před 4 měsíci | |
| README.md | před 4 měsíci | |
README.md
TinyRenderer
光栅化
求重心
重心坐标 (α, β, γ) 表示点 P 可以表示为三角形三个顶点A、B、C的加权和:P = αA + βB + γC,其中 α + β + γ = 1
如果点P在三角形内部,则满足:0 ≤ α, β, γ ≤ 1
通过重心坐标,即可知道某个点是否在三角形内部
α·A_x + β·B_x + γ·C_x = P_x
α·A_y + β·B_y + γ·C_y = P_y
α + β + γ = 1
对应的矩阵表现形式是
| A_x B_x C_x | | α | | P_x |
| A_y B_y C_y | × | β | = | P_y |
| 1 1 1 | | γ | | 1 |
设矩阵 M 为
| A_x B_x C_x |
M = | A_y B_y C_y |
| 1 1 1 |
需要求解的是向量 [α, β, γ]ᵀ ,使得: M × [α, β, γ]ᵀ = [P_x, P_y, 1]ᵀ
解为:[α, β, γ]ᵀ = M⁻¹ × [P_x, P_y, 1]ᵀ
vec3 barycentric(const vec2 tri[3], const vec2 P) {
mat<3,3> ABC = {{ {tri[0].x, tri[0].y, 1.}, {tri[1].x, tri[1].y, 1.}, {tri[2].x, tri[2].y, 1.} }};
if (ABC.det()<1) return {-1,1,1};
return ABC.invert_transpose() * vec3{P.x, P.y, 1.};
}
透视矫正
| 参考文章 | 链接 |
|---|---|
| 透视矫正插值 | https://zhuanlan.zhihu.com/p/403259571 |
| Perspective Correct Interpolation | https://www.cs.ucr.edu/~craigs/courses/2018-fall-cs-130/lectures/perspective-correct-interpolation.pdf |
| 贴图 | 渲染效果 |
|---|---|
 |
 |
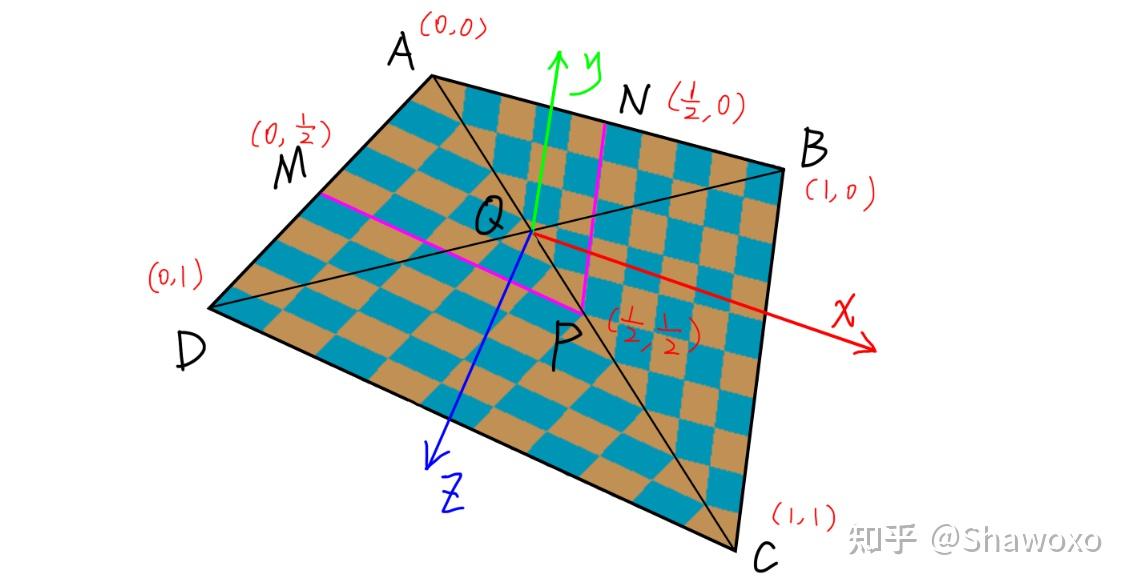
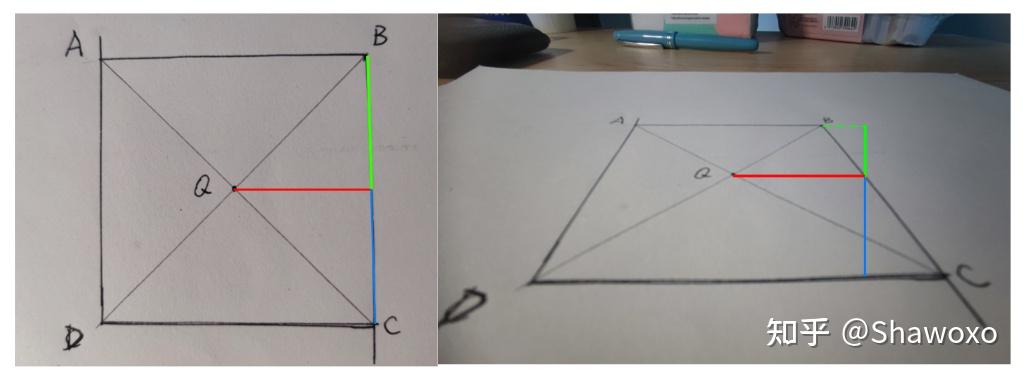
示意图
由于透视的问题,明明 Q 点是 AC 中点;但是由于透视的存在,看起来 P 点才像是 AC 中点
在坐标点通过 MVP 矩阵变化到屏幕空间中,会将 P 点的 UV 坐标设置为 (1/2, 1/2),最终导致显示问题
可以通过 顶点的世界坐标 和 目标点的屏幕坐标,计算得到目标点对应平面上的 世界坐标
首先考虑 二维 的情况,由简入繁
通过相似计算
$$ \frac{n}{1-n} = \frac{|AG|}{|BK|} = \frac{|A'P'| * \frac{Z_1}{c}}{|B'P'|\frac{Z_2}{c}} = \frac{m*Z_1}{(1-m)*Z_2} $$
对左右两边取倒
$$ \frac{1}{n} - 1 = \frac{(1-m)*Z_2}{m*Z_1} \ n = \frac{m*Z_1}{(1-m)*Z_2 + m*Z_1} $$
由于 A'、B'、P' 都是已知的屏幕坐标点,所以可以很轻松的计算得到 m 的值,进而计算得到 n 的值
P 的坐标可以通过 P = (1-n) * A + n * B 得到,进而得到 P 的坐标计算公式
假设 A 点坐标为 (0, Y1, Z1) ,B 点坐标为 (0, Y2, Z2)
$$ Z_n = (1-n) * Z_1 + n * Z_2 \\ Z_n = \frac{(1-m) * Z_2}{(1-m)*Z_2 + m*Z_1} * Z_1 + \frac{m*Z_1}{(1-m)*Z_2 + m*Z_1} * Z_2 \\ Z_n = \frac{1}{\frac{1-m}{Z_1} + \frac{m}{Z_2}} $$
带入到三维场景中
$$ Z_n = \frac{1}{\frac{1-u-v}{Z_1} + \frac{u}{Z_2} + \frac{v}{Z_3}} $$
u、v 满足 P = (1-u-v)*A + u*B + v*C