添加凸多边形判断和拆分

Navigation/README.md

@@ -28,7 +28,7 @@
 | Corwds In A Polygon Soup: Next-Gen Path Planning | David Miles | 2006 |
 | Recast Navigation | Mikko Mononen | 2008 |
 
-### **Meadow Mapping**
+### Meadow Mapping
 
 Ronald C. Arkin 是一位美国计算机科学家，他在 1987 年发表了一篇论文 **《Path planning for a vision-based autonomous robot》** ，介绍了 `Meadow mapping` 的原理和实现
 
@@ -45,7 +45,7 @@ Meadow mapping 是一种用于生成导航网格的方法，它将自由空间
 1. 凸多边形内任意俩点连接不会超出多边形区域
 2. 凸多边形边上的点便于做寻路最小单位
 
-凸多边形内部不需要寻路
+**凸多边形内部不需要寻路**
 
 我们只需要将世界划分成多个凸多边形，那么就只需要研究凸多边形之间如何连通即可，凸多边形内部直接一根直线连接即可
 
@@ -69,7 +69,7 @@ Meadow mapping 是一种用于生成导航网格的方法，它将自由空间
 2. 如何区域划分凸多边形
 3. 如何进行路径查询
 
-**区域划分凸多边形**
+#### 区域划分凸多边形
 
 ![](Image/001.png)
 
@@ -77,6 +77,104 @@ Meadow mapping 是一种用于生成导航网格的方法，它将自由空间
 
 如果区域不是凸多边形，则找到一个凹的角（>180°），尝试将其与多边形内部其他的点连接起来，这个时候会得到两个新的区域，也就是上图的 A 和 B，然后对这两个区域再进行相同的算法，如此一来整个场景就都是凸多边形
 
-- 如何判断一个多边形是凸多边形
+- 如何判断一个多边形是凸多边形？
+
+检查是否存在大于 180° 的角
+
+规定凸多边形节点顺序按照**逆时针**走
+
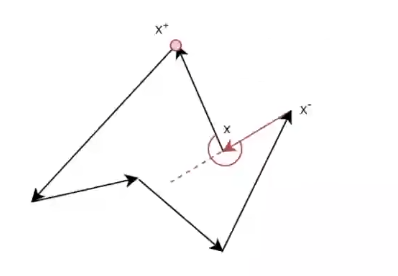
+向量 (x-, x) 和向量 (x, x+) 进行**叉乘**，可以判断点 x+ 在向量 (x-, x) 的左边还是右边。**叉乘**的结果如果是正数那么就是在**左边**，反之在**右边**
+
+![](Image/002.png)
+
+以上图为例，点 x+ 在向量 (x-, x) 的**右边**，那么这个点的角度大于 180°
+
+![](Image/003.png)
+
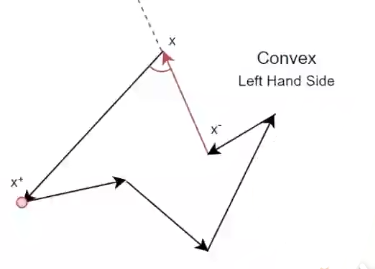
+以上图为例，点 x+ 在向量 (x-, x) 的**左边**，那么这个点的角度小于180°
+
+通过上面的发现，我们只需要遍历凸多边形所有的点，即可判断每个点的角度是否大于180°，以此判断该多边形是否是凸多边形
+
+- 如何将大于 180° 角的点连接到多边形其他**可见**顶点上？
+
+**检查所有多边形节点与之连线是否为对角线**
+
+- 对角线的要求
+  - 条件1：不与多边形的边相交
+  - 条件2：在多边形内部
+
+![](Image/004.png)
+
+> 上图中 af 与 gh 相交，不符合条件1
+> 上图中 ag 不在多边形内部，不符合条件2
+
+以凹点 a 为例，对 a 点来说 g、f 两点就是不可见的，因为 ag 连线完全在多边形外，af 连线与 gh 连线相交
+
+> 这里推荐一本书 《Computational Geometry in C》 
+
+如何判断 af 和 gh 线段相交？
+
+高中数学提供的解决方案就是点斜式求斜率，然后进行计算。但是在计算机中，直接根据 `k = (y2 - y1) / (x2 - x1)` 算出来使用 `double` 存储可能存在精度问题，或者除 0 错误
+
+这里依然使用叉乘的思想
+
+![](Image/005.png)
+
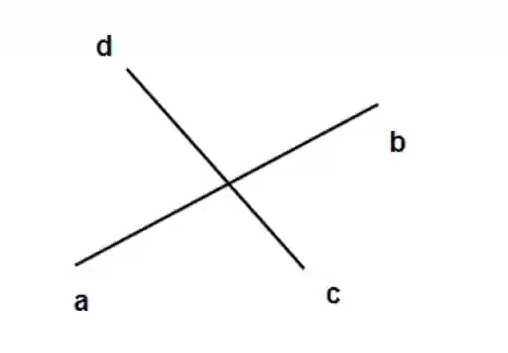
+如果 a、b 两点在 dc 线段的两端，并且 d、c 两点在 ab 线段的两端，那么线段 ab 和 dc 相交
+
+```cpp
+bool isCross(Vector2D a, Vector2D b, Vector2D c, Vector2D d) {
+    // c、d 两点在线段 ab 的两端
+    bool cd_cross = isLeft(a, b, c) ^ isLeft(a, b, d);
+    // a、b 两点在线段 cd 的两端
+    bool ab_cross = isLeft(c, d, a) ^ isLeft(c, d, b);
+    return cd_cross && ab_cross;
+}
+```
+
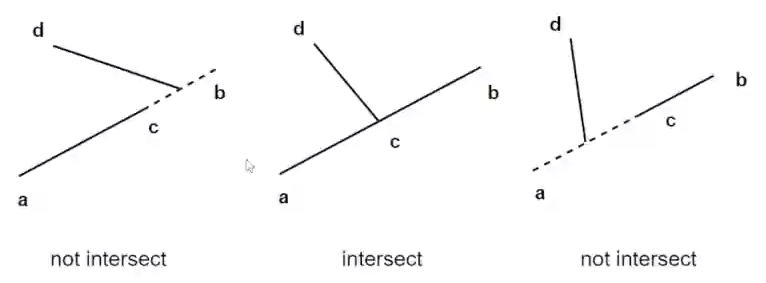
+上述代码使用异或来判断是否满足两点在线段两端的判断，如果两点都在右边或者都在左边，那么**异或**的结果就是 `false`，如果两点一个在左边一个在右边则**异或**的结果是 `true`
+
+![](Image/006.png)
+
+但是上述解法无法处理共线问题，比如上图所示，点 c 在线段 ab 上，所以需要**额外判断共线问题**
+
+所以判断线段是否相交的大概算法如下
+
+```cpp
+bool isCross(Vector2D a, Vector2D b, Vector2D c, Vector2D d) {
+    if (c 与 ab 共线) {
+        return c 是否在线段 ab 上;
+    }
+    if (d 与 ab 共线) {
+        return d 是否在线段 ab 上;
+    }
+    if (a 与 cd 共线) {
+        return a 是否在线段 cd 上;
+    }
+    if (b 与 cd 共线) {
+        return b 是否在线段 cd 上;
+    }
+    // c、d 两点在线段 ab 的两端
+    bool cd_cross = isLeft(a, b, c) ^ isLeft(a, b, d);
+    // a、b 两点在线段 cd 的两端
+    bool ab_cross = isLeft(c, d, a) ^ isLeft(c, d, b);
+    return cd_cross && ab_cross;
+}
+```
+
+> 判断 c 是否与 ab 共线，可以通过 c 到直线 ab 的距离来判断，小于一个极小值就算共线  
+
+> 判断 c 是否在线段 ab 上则直接通过坐标计算即可
+
+通过上面判断线段相交可以处理处理线段 af 与 gh 的情况，那么如何处理 ag 线段在多**边形外**的情况呢？
+
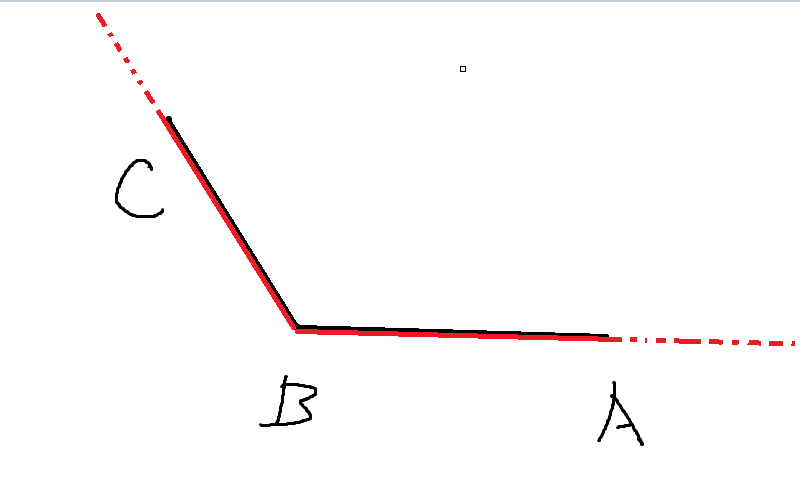
+我们先定义什么是**锥形**
+
+![](Image/007.png)
+
+以上图为例，直线 BA 和 直线 BC 就可以构成一个**锥形**
+
+我们先分类讨论，如果是凸点(小于 180° 角的点)，那么对角线在锥形范围内；如果是凹点(大于 180° 角的点)，那么对角线在锥形范围外
+
+所以算法的重点在如何判断**直线在锥形范围内**
 
-检查是否存在大于 180° 的角