|
|
@@ -30,15 +30,24 @@ https://latex.codecogs.com/svg.latex?\vec{A}=(^{x}_{y})\\\vec{A}^T=(x,y)\\\lVert
|
|
|
### 点乘
|
|
|
|
|
|
$$
|
|
|
-\vec{A} = (^{x} _{y}) \\
|
|
|
-\vec{A}^T = (x, y) \\
|
|
|
-\lVert \vec{A} = \sqrt{x ^2 + y^2} \rVert \\
|
|
|
+\vec{A} = (^{x} _{y})
|
|
|
+$$
|
|
|
+
|
|
|
+$$
|
|
|
+\vec{A}^T = (x, y)
|
|
|
+$$
|
|
|
+
|
|
|
+$$
|
|
|
+\lVert \vec{A} = \sqrt{x ^2 + y^2} \rVert
|
|
|
$$
|
|
|
|
|
|
向量之间的点乘
|
|
|
|
|
|
$$
|
|
|
-\vec{A} \cdot \vec{B} = \lVert \vec{A} \rVert * \lVert \vec{B} \rVert * \cos \theta \\
|
|
|
+\vec{A} \cdot \vec{B} = \lVert \vec{A} \rVert * \lVert \vec{B} \rVert * \cos \theta
|
|
|
+$$
|
|
|
+
|
|
|
+$$
|
|
|
\cos \Theta = \frac{\vec{A} \cdot \vec{B}}{\lVert \vec{A} \rVert * \lVert \vec{B} \rVert}
|
|
|
$$
|
|
|
|
|
|
@@ -2173,7 +2182,7 @@ Shadow Mapping可以处理硬阴影的情况:即一个点要么在阴影中,
|
|
|
|
|
|
### 加速计算光线与物体表面的求交 (Accelerating Ray-Surface Intersection)
|
|
|
|
|
|
-计算光照最暴力的做法,每个像素打出的光线都要与所有的物体,所有的三角形计算交点,并且光线每经过一次 反射/折射 都要计算新的光线与每个物体的三角形的交点
|
|
|
+计算光照最暴力的做法,每个像素打出的光线都要与**所有的物体**,**所有的三角面**计算交点,并且光线每经过一次 反射/折射 都要计算新的光线与每个物体的三角形的交点
|
|
|
|
|
|
如果真的是上面这种暴力做法,计算效率就特别低
|
|
|
|
|
|
@@ -2219,4 +2228,76 @@ $t_{quit} = max(t_{x_{max}}, t_{y_{max}}, t_{z_{max}})$
|
|
|
- $t_{enter}$ 小于0, ${t_{quit}}$ 大于0,则表示 光源 在碰撞盒 内部
|
|
|
- 如果 $t_{enter}$ 小于 ${t_{quit}}$,并且 $t_{quit}$ 大于 0, 则表示 光线 与 碰撞盒 相交
|
|
|
|
|
|
+#### AABB帮助加速求交计算
|
|
|
+
|
|
|
+1. 找到包围盒
|
|
|
+
|
|
|
+
|
|
|
+
|
|
|
+> 假设上图外框一个包围盒包住了5个圆
|
|
|
+
|
|
|
+2. 对包围盒 划分网格 并 标记与物体相交的网格 (预处理)
|
|
|
+
|
|
|
+
|
|
|
+
|
|
|
+> 上图右上角还有一个网格没有标记出来
|
|
|
+
|
|
|
+3. 光线追踪
|
|
|
+
|
|
|
+
|
|
|
+
|
|
|
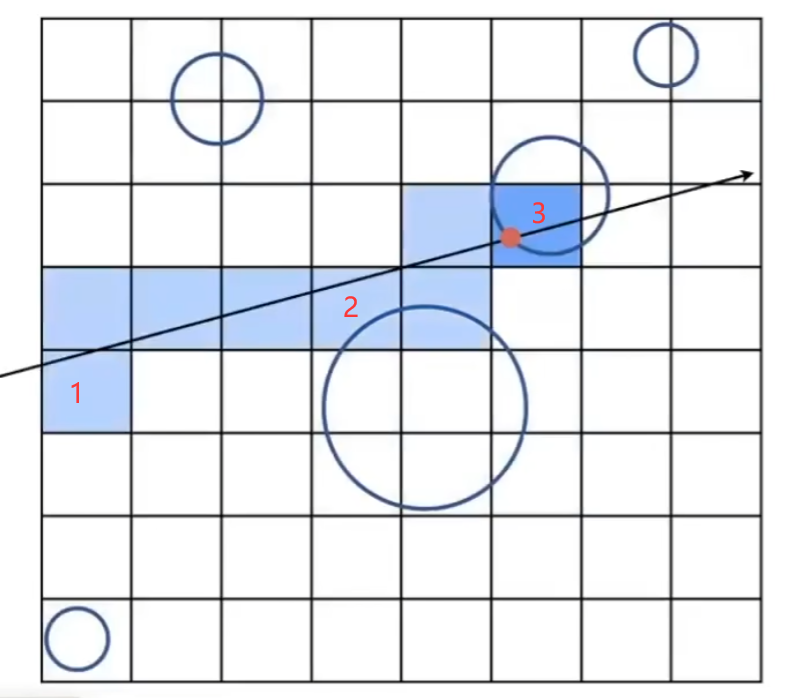
+这里将光线与网格的碰撞分成了三种情况
|
|
|
+
|
|
|
+- 网格1: 与光线相交,但是网格内并没有物体,所以无需处理
|
|
|
+- 网格2: 与光线相交,并且网格内存在物体,需要计算一次光线与物体相交的判断,计算后发现光线与物体不相交,无需处理
|
|
|
+- 网格3: 与光线相交,并且网格内存在物体,需要计算一次光线与物体相交的判断,计算后发现光线与物体相交,需要计算颜色
|
|
|
+
|
|
|
+光线与网格相交的计算很快,与物体相交的计算很慢
|
|
|
+
|
|
|
+至于与哪些网格相交,举个例子就是这里的**光线的方向是右上方**,那么下一个与光线相交的格子要么是**当前格子的右边**,要么是**当前格子的上面**
|
|
|
+
|
|
|
+通过上述方法可以加速计算光线与物体相交的计算,但是存在一个问题,对包围盒进行网格划分的**密度应该如何设置?**
|
|
|
+
|
|
|
+这里存在两个极端情况
|
|
|
+
|
|
|
+1. 不做任何划分 -> 没有任何效果
|
|
|
+2. 划分的很密集 -> 与网格相交的计算量与直接计算所有物体相交的计算量相近
|
|
|
+
|
|
|
+经过测试 网格数量 = 物体数量 * 27 是一个比较好的效果,常数27
|
|
|
+
|
|
|
+使用网格划分对于物体比较均匀划分的场景应用比较合适,但是对于中空比较多的场景就不太合适,比如篮球场,大部分都是空的,这样空白网格过多也会造成许多无效计算
|
|
|
+
|
|
|
+#### 空间划分
|
|
|
+
|
|
|
+针对上面物体分布不均匀的状况,可以把空的地方不划分,物体多的地方多划分
|
|
|
+
|
|
|
+
|
|
|
+
|
|
|
+- Oct-Tree 八叉树 (三维空间 一个立方体切成8块, 二维空间 一个正方形分成4份)
|
|
|
+- KD-Tree
|
|
|
+- BSP-Tree
|
|
|
+
|
|
|
+对于上述的树形结构,一般物体的信息存储在**叶子节点**中,**非叶子节点**存储网格对应的坐标、大小等信息
|
|
|
+
|
|
|
+
|
|
|
+
|
|
|
+> 上述左图为空间划分,右图为树形结构
|
|
|
+
|
|
|
+1. 一根光线发出
|
|
|
+2. A区域对应的叶子节点中存储了A区域的坐标和大小,判定光线穿过了A区域
|
|
|
+3. A节点下的左节点1 判断是否与光线相交,发现相交,与1区域所有物体求交
|
|
|
+4. A节点下的右节点B 判断是否与光线相交,发现相交,由于B节点非叶子节点,继续判断B节点下的左右叶子节点
|
|
|
+5. B节点下的左节点2 判断是否与光线相交,发现相交,与2区域所有物体求交
|
|
|
+6. B节点下的右节点C 判断是否与光线相交,发现相交,由于C节点非叶子节点,继续判断C节点下的左右叶子节点
|
|
|
+7. C节点下的左节点D 判断是否与光线相交,发现相交,由于D节点非叶子节点,继续判断D节点下的左右叶子节点
|
|
|
+8. D节点下的左节点4 判断是否与光线相交,发现相交,与4区域所有物体求交
|
|
|
+9. D节点下的右节点5 判断是否与光线相交 发现不相交 不做处理 跳过
|
|
|
+10. C节点下的右节点3 判断是否与光线相交 发现相交,与3区域所有物体求交
|
|
|
+11. 结束
|
|
|
+
|
|
|
+按照上图,虽然成功进行了空间划分,但是也暴露的一些问题
|
|
|
+
|
|
|
+1. 有些物体横框了多个包围盒,也就是说每个包围盒叶子节点都要存一份该物体,但其实最好一个物体就存在一个叶子节点中
|
|
|
+2. 如何计算物体与包围盒相交,这个计算其实比较复杂
|
|
|
+
|
|
|
# 动画模拟、仿真
|