transition

图形学/图形学.md

@@ -1,7 +1,7 @@
 <!--
  * @Author: your name
  * @Date: 2021-10-01 11:33:27
- * @LastEditTime: 2022-02-19 17:04:58
+ * @LastEditTime: 2022-02-19 20:08:55
  * @LastEditors: Please set LastEditors
  * @Description: In User Settings Edit
  * @FilePath: D:\MarkdownLog\图形学.md
@@ -25,11 +25,11 @@
 
 ### 点乘
 
-```math
+$$
 \vec{A} = (^{x} _{y}) \\
 \vec{A}^T = (x, y) \\
 \lVert \vec{A} = \sqrt{x ^2 + y^2} \rVert \\
-```
+$$
 
 向量之间的点乘 
 
@@ -169,34 +169,34 @@ $$
 
 将单位向量按y轴对称的操作：
 $$
-\begin{pmatrix}
+\begin{bmatrix}
     -1 & 0 \\
     0 & 1
-\end{pmatrix} 
+\end{bmatrix} 
 *
-\begin{pmatrix}
+\begin{bmatrix}
     x\\
     y
-\end{pmatrix}
+\end{bmatrix}
 =
-\begin{pmatrix}
+\begin{bmatrix}
     -x \\
     y
-\end{pmatrix}
+\end{bmatrix}
 $$
 
 矩阵的转置:行和列互换
 
 $$
-\begin{pmatrix}
+\begin{bmatrix}
     1 & 2 \\
     3 & 4 \\
     5 & 6 
-\end{pmatrix} ^T = 
-\begin{pmatrix}
+\end{bmatrix} ^T = 
+\begin{bmatrix}
     1 & 3 & 5 \\
     2 & 4 & 6 
-\end{pmatrix}
+\end{bmatrix}
 \\
 (AB)^T = B^T * A^T
 $$
@@ -205,11 +205,11 @@ $$
 
 $$
 I_{3\times3} = 
-\begin{pmatrix}
+\begin{bmatrix}
     1 & 0 & 0 \\
     0 & 1 & 0 \\
     0 & 0 & 1
-\end{pmatrix}
+\end{bmatrix}
 $$
 
 矩阵的逆：矩阵A乘矩阵B得到单位矩阵，则成B是A的逆，写作$A^{-1}$
@@ -220,12 +220,12 @@ $AA^{-1} = I$、$(AB)^{-1} = B^{-1} * A^{-1}$
 
 $$
 \vec{a} \cdot \vec{b} = \vec{a}^T\vec{b}=
-\begin{pmatrix}
+\begin{bmatrix}
     x_a & y_a & z_a
-\end{pmatrix} 
-\begin{pmatrix}
+\end{bmatrix} 
+\begin{bmatrix}
     x_b \\ y_b \\ z_b
-\end{pmatrix}
+\end{bmatrix}
 = \left( x_a*x_b + y_a*y_b + z_a*z_b \right)
 $$
 
@@ -233,20 +233,318 @@ $$
 
 $$
 \vec{a} \times \vec{b} = A^*\vec{b} = 
-\begin{pmatrix}
+\begin{bmatrix}
     0 & -z_a & y_a \\
     z_a & 0 & -x_a \\
     -y_a & x_a & 0
-\end{pmatrix}
-\begin{pmatrix}
+\end{bmatrix}
+\begin{bmatrix}
     x_b \\ y_b \\ z_b
-\end{pmatrix}
+\end{bmatrix}
 $$
 
 > $A^*$是$\vec{a}$的dual matrix
 
 ## 变换
 
+### 仿射变换
+
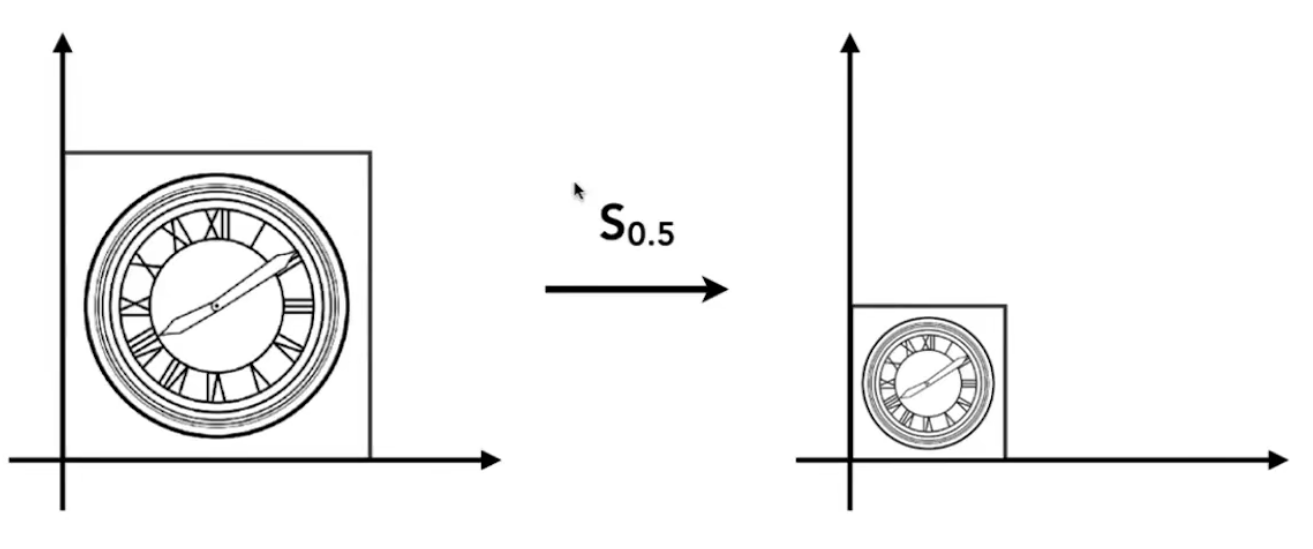
+#### 伸缩变换(Scale)
+
+![缩放](./Image/4.png)
+
+$$
+x^` = sx\\
+y^` = sy\\
+\Rightarrow \\
+\begin{bmatrix}
+    x^` \\ y^`
+\end{bmatrix}
+= 
+\begin{bmatrix}
+    s & 0 \\
+    0 & s 
+\end{bmatrix}
+\begin{bmatrix}
+    x \\ y
+\end{bmatrix}
+$$
+
+### 镜像
+
+![缩放](./Image/5.png)
+
+$$
+x^` = -x\\
+y^` = y\\
+\Rightarrow \\
+\begin{bmatrix}
+    x^` \\ y^`
+\end{bmatrix}
+= 
+\begin{bmatrix}
+    -1 & 0 \\
+    0 & 1 
+\end{bmatrix}
+\begin{bmatrix}
+    x \\ y
+\end{bmatrix}
+$$
+
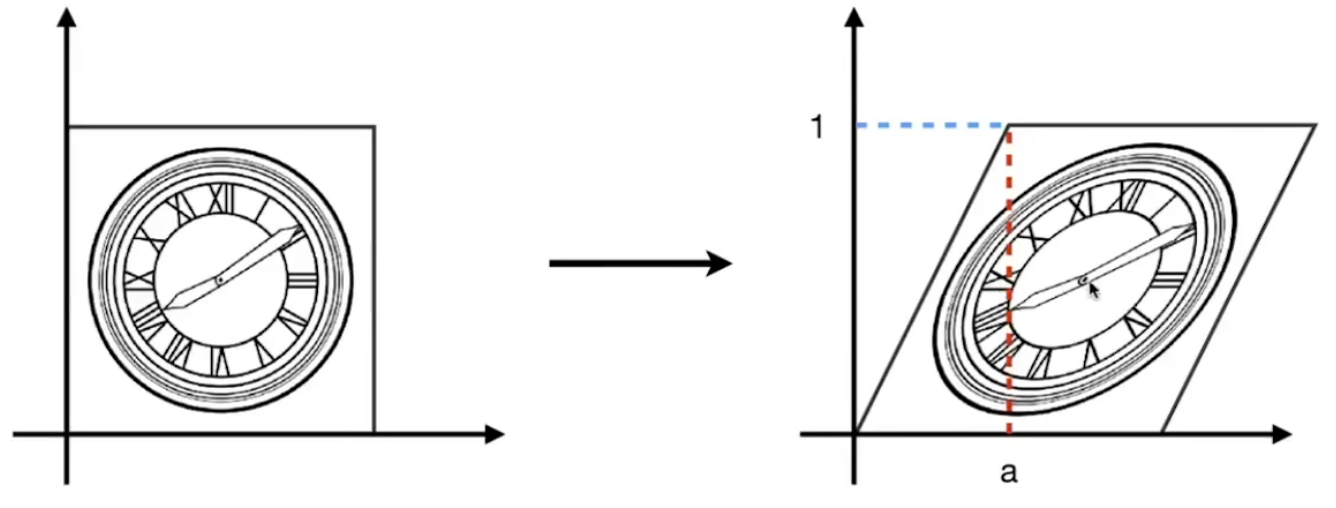
+#### 切变
+
+![切变](./Image/6.png)
+
+$$
+x^` = x + a*y\\
+y^` = y\\
+\Rightarrow \\
+\begin{bmatrix}
+    x^` \\ y^`
+\end{bmatrix}
+= 
+\begin{bmatrix}
+    1 & a \\
+    0 & 1 
+\end{bmatrix}
+\begin{bmatrix}
+    x \\ y 
+\end{bmatrix}
+$$
+
+#### 旋转(Rotate)
+
+**默认绕原点逆时针旋转**
+
+![旋转](./Image/7.png)
+
+公式推导  
+- 右下角点坐标(1, 0)=>($\cos\Theta, \sin\Theta$)
+- 左上角点坐标(0, 1)=>($-\sin\Theta, \cos\Theta$)
+
+$$
+\left(x^`, y^`\right)
+\Longrightarrow
+\begin{bmatrix}
+    A & B \\
+    C & D 
+\end{bmatrix}
+\begin{bmatrix}
+    x \\ y
+\end{bmatrix}\\
+带入x=1, y=0, x^`=\cos\Theta, y^`=\sin\Theta\\
+得: A = \cos\Theta , C = \sin\Theta\\
+带入x=0, y=1, x^`=-\sin\Theta, y^`=\cos\Theta\\
+得: B = -\sin\Theta, D = \cos\Theta
+$$
+
+#### 平移(Transiation)
+
+![平移](./Image/8.png)
+
+- $x^` = x + t_x$
+- $y^` = y + t_y$
+
+$$
+\begin{bmatrix}
+    x^` \\ y ^ `
+\end{bmatrix}
+=
+\begin{bmatrix}
+    1 & 0 \\
+    0 & 1 
+\end{bmatrix}
+\begin{bmatrix}
+    x \\ y
+\end{bmatrix}
++
+\begin{bmatrix}
+    t_x \\ t_y
+\end{bmatrix}
+$$
+
+很明显，这个**平移**的坐标无法通过一个矩阵就表示出来，这个时候就需要引入**齐次矩阵**
+
+> **齐次矩阵**就是将一个原本是n维的向量用一个n+1维向量来表示
+
+$$
+\begin{bmatrix}
+    x^` \\ y ^ ` \\ 1
+\end{bmatrix}
+=
+\begin{bmatrix}
+    1 & 0 & t_x \\
+    0 & 1 & t_y \\
+    0 & 0 & 1
+\end{bmatrix}
+\begin{bmatrix}
+    x \\ y \\ 1
+\end{bmatrix}
+=
+\begin{bmatrix}
+    x + t_x \\ y + t_y \\ 1
+\end{bmatrix}
+$$
+
+通过齐次坐标矩阵就可以使用一个矩阵来表示线性变换，**为了保证变换矩阵的一致性**，所以上面讲的**所有矩阵都需要转换成齐次矩阵**
+
+在其次坐标中，点使用$\begin{pmatrix}
+    x \\ y \\ 1
+\end{pmatrix}$
+来表示，向量使用$\begin{pmatrix}
+    x \\ y \\ 0
+\end{pmatrix}$
+来表示
+
+- 向量 + 向量 = 向量  
+- point - point = 向量
+- point + vector = point
+- point + point = 两点的中点
+
+为什么point + point的结果是两个点的中点
+
+$$
+A = \begin{pmatrix}
+    x \\ y \\ w
+\end{pmatrix}
+=
+\begin{pmatrix}
+    x / w \\ y / w \\ 1
+\end{pmatrix}
+\\
+B = \begin{pmatrix}
+    a \\ b \\ c
+\end{pmatrix}
+=
+\begin{pmatrix}
+    a / c \\ b / c \\ 1
+\end{pmatrix}
+\\
+A + B = 
+\begin{pmatrix}
+    x/w + a/c \\ y/w + b/c \\ 2
+\end{pmatrix}
+=
+\begin{pmatrix}
+    \frac{x}{2w} + \frac{a}{2c} \\
+    \frac{y}{2w} + \frac{b}{2c} \\
+    1
+\end{pmatrix}
+$$
+
+#### 总和
+
+$$
+Scale \Longrightarrow
+S(s_x, s_y) = 
+\begin{pmatrix}
+    s_x & 0 & 0 \\
+    0 & s_y & 0 \\
+    0 & 0 & 1
+\end{pmatrix}
+\\
+Rotation \Longrightarrow
+R(\Theta) = 
+\begin{pmatrix}
+    \cos\Theta & -\sin\Theta & 0 \\
+    \sin\Theta & \cos\Theta & 0 \\
+    0 & 0 & 1
+\end{pmatrix}
+\\
+Translation \Longrightarrow
+T(t_x, t_y) = 
+\begin{pmatrix}
+    1 & 0 & t_x \\
+    0 & 1 & t_y \\
+    0 & 0 & 1
+\end{pmatrix}
+$$
+
+### 组合变换
+
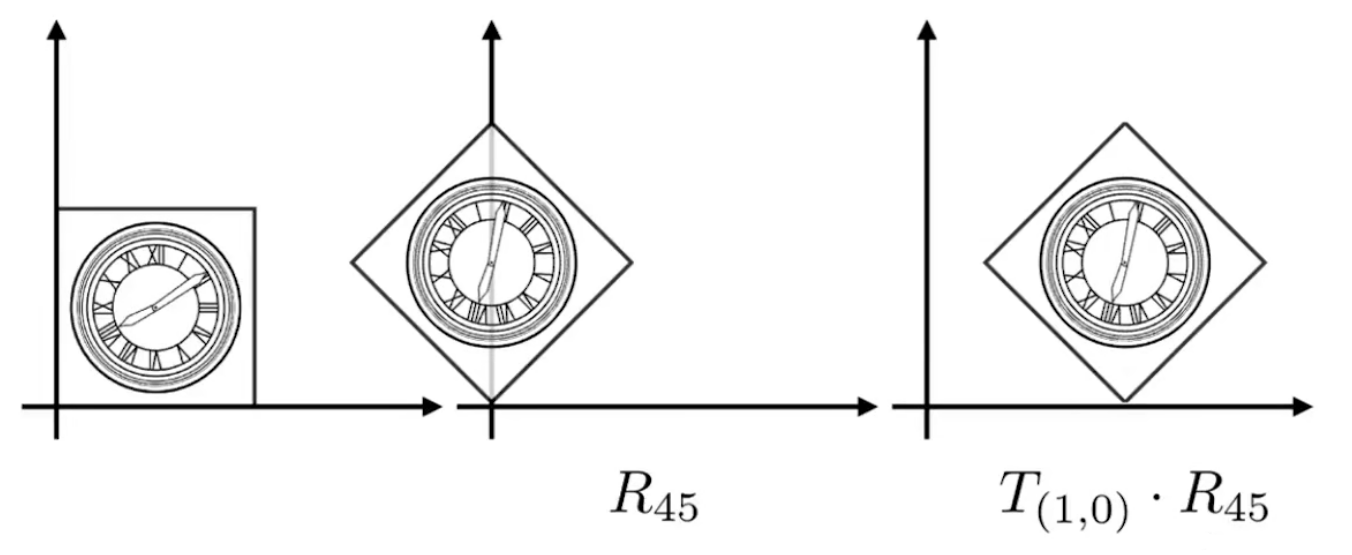
+- 图1
+![图1](./Image/10.png)
+
+- 图2
+![图2](./Image/11.png)
+
+> 旋转默认绕原点，逆时针旋转  
+
+比较上述两张图片，可以发现先旋转再平移 与 先平移再旋转 得到的结果是不同的，对应的理解就是**矩阵的乘法**，矩阵乘法不满足交换律
+
+为了得到图1的效果，我们需要先旋转45°，再向X轴正方向平移1一个单位
+
+$$
+T_{(1， 0)} \cdot R_{45} \cdot \begin{bmatrix}
+    x \\ y \\ 1
+\end{bmatrix}
+= 
+\begin{bmatrix}
+    1 & 0 & 1 \\
+    0 & 1 & 0 \\
+    0 & 0 & 1 
+\end{bmatrix}
+\begin{bmatrix}
+    \cos45° & -\sin45° & 0 \\
+    \sin45° & \cos45° & 0 \\
+    0 & 0 & 1 
+\end{bmatrix}
+\begin{bmatrix}
+    x \\ y \\ 1
+\end{bmatrix}
+$$
+
+前面提过向量一般放在矩阵乘法的最右边，并且根据矩阵具有结合律，上述式子可以理解为先计算$R_{45}$与$\begin{bmatrix}x\\y\\1\end{bmatrix}$，再计算与$T_{(1, 0)}$的乘法
+
+但是，根据矩阵的结合律，我们可以先把前面的矩阵的计算结果得出最终变换矩阵，最后与向量相乘
+
+$$
+A_n(...A_2(A_1(X)) = 
+\underbrace{A_n...A_2 \cdot A_1}_{先计算} \cdot \begin{pmatrix}
+    x \\ y \\ 1
+\end{pmatrix}
+$$
+
+### 变换的分解
+
+![变换的分解](./Image/12.png)
+
+如果想让图片围绕左下角旋转，而不是原点选择，可以采用的解法是 
+
+左下角移动到原点 => 绕原点旋转 => 左下角移动到起始位置  
+
+### 三位空间的变换
+
+point : $\begin{pmatrix}
+    x \\ y \\ z \\ 1
+\end{pmatrix}$  
+vector : $\begin{pmatrix}
+    x \\ y \\ z \\ 0
+\end{pmatrix}$
+
+$$
+
+\begin{pmatrix}
+    x^` \\ y^1 \\ z^` \\ 1
+\end{pmatrix}
+=
+\begin{pmatrix}
+    a & b & c & t_x \\
+    d & e & f & t_y \\
+    g & h & i & t_z \\
+    0 & 0 & 0 & 1
+\end{pmatrix}
+\begin{pmatrix}
+    x \\ y \\ z \\ 1
+\end{pmatrix}
+$$
+
+### 逆变换
+
+![逆变换](./Image/9.png)
+
+逆变换就是把之前的操作反向来一次，对应的就是矩阵中的逆矩阵 
+
 
 
 # 光栅化