feat: 添加光照的一些介绍

图形学/DirectX学习/README.md

@@ -2663,7 +2663,129 @@ cbuffer cbSettings : register(b0) {
 
 光照和阴影可以帮助我们感受到物体的实体形状，还展现出物体的体积感。事实上，视觉上对世界的感知依靠的是光照及其与材质的交互。因此，在生成逼真场景的众多问题之中，首先要解决的是遵循自然规律实现精确的光照模型(lighting model)
 
+#### 光照与材质交互
 
+在开启光照的同时，不再直接指出顶点和颜色，而是指定**材质**与光照，在运用光照方程(`lighting equation`)基于两者的交互来计算顶点颜色
+
+**材质**可以看作是确定光照与物体如何交互的属性集。此属性集中的属性有：表面反射光和吸收光的颜色、表面下材质的折射率、表面的光滑度以及表面的透明度
+
+> 通过指定材质属性，可以未真实世界中的木材、石头、玻璃、金属等不同种类的表面进行建模
+
+后面的例子采用的光照模型均为**局部光照模型**：每个物体的光照皆独立于其他物体，在处理光照的过程中仅考虑光源直接发出的光线，忽略来自场景中其他物体所反弹来的光
+
+反之还有**全局光照模型**：除了考虑有光源直接发出的光，还要顾及场景中其他物体反弹来的间接光
+
+#### 法向量
+
+平面法线是一种描述多边形朝向的单位向量。曲面法线是一种垂直于曲面上一点处切面的单位向量
+
+![](Image/035.png)
+
+对于光照计算来说，需要通过三角形网格曲面上每一点处的曲面法线来确定找到对应点上的角度。
+
+为了求出曲面法线，需要先指定位于网格顶点处的曲面法线(**顶点法线**)，为了获得三角形网格每个点处的近似曲面法线，在三角形进行光栅化的过程中对这些顶点进行插值计算
+
+![](Image/036.png)
+
+针对三角形 $p_0p_1p_2$ ，那么三角形两边的向量为 $u=p_1-p_0$ 和 $v=p_2-p_0$，那么三角形的平面法线为 $n=\frac{u \times v}{\left \| u \times v \right \| }$
+
+```hlsl
+XMVECTOR ComputeNormal(FXMVECTOR p0, FXMVECTOR p1, FXMVECTOR p2) {
+	XMVECTOR u = p1 - p0;
+	XMVECTOR v = p2 - p1;
+	XMVector3Cross(u, v);
+}
+```
+
+对于可微的光滑曲面而言，可以利用微积分方面的知识来求出曲面点处的法线。三角形网格运用一种被称为**求顶点法线平均值**的计算方法
+
+![](Image/037.png)
+
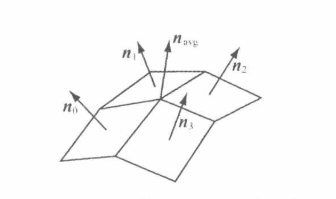
+通过对网格中共享顶点 v 的多边形的平面法线取平均值，从而获得网格中顶点 v 处的顶点法线 n
+
+$n_{avg} = \frac{n_0+n_1+n_2+n_3}{\left \| n_0+n_1+n_2+n_3 \right \|}$
+
+> 这里已经得到了规范化的向量，无需额外除以4
+
+为了得到更精精确的结果，还可以采用更加复杂的求平均值方法，比如根据多边形的面积来确定权重，以求取加权平均值
+
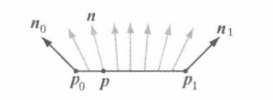
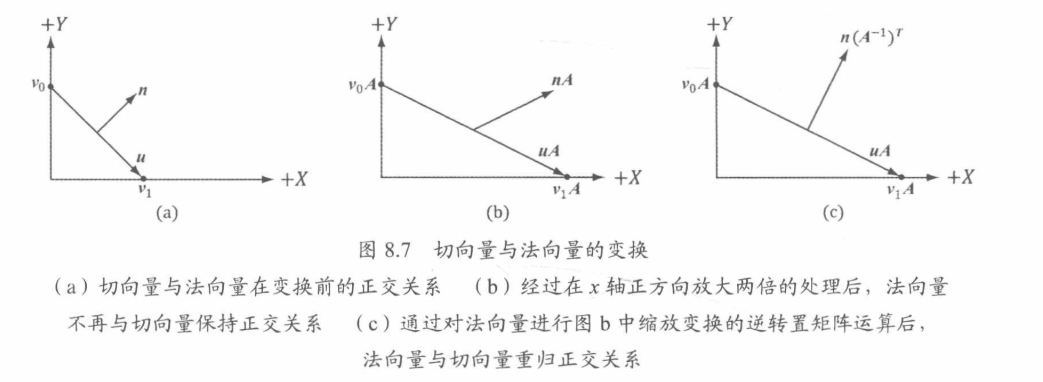
+针对 $v_0$ 和 $v_1$ 两点，向量 $v=v_1-v_0$ 得到切向量 v，对应的法向量为 n
+
+![](Image/038.png)
+
+如果对 $n_0$ 和 $n_1$ 进行非等比缩放变换 A，也就是上图的 a 和 b 两部分，可以法线变换后的切向量 $uA = v_1A - v_0A$ 不能与 $nA$ 向量正交
+
+所以当切向量非等比缩放后，不能单纯的将缩放变化矩阵乘以法向量
+
+1. 切向量正交于法向量： $u \cdot n = 0$
+2. 将点积改写为矩阵乘法： $un^T = 0$
+3. 插入单位矩阵 $I = AA^{-1}$： $u(AA^{-1})n^{T} = 0$
+4. 根据矩阵乘法的结合律： $(uA)(A^{-1}n^{T}) = 0$
+5. 根据转置矩阵的特性 $(A^T)^T = A$ 得到：$(uA)((A^{-1}n^{T})^T)^T = 0$
+6. 根据转置矩阵的性质 $(AB)^T = B^TA^T$ 得到： $(uA)(n(A^{-1})^T)^T = 0$
+7. 再将矩阵乘法改为点积的形式： $uA \cdot n(A^{-1})^T = 0$
+
+通过上述公式推导，得到变换后的切向量 $uA$ 与 $n(A^{-1})^T$ 正交，所以变换后的法向量 u 要乘以 $(A^{-1})^T$ 矩阵
+
+#### 参与光照计算的一些关键向量
+
+![](Image/039.png)
+
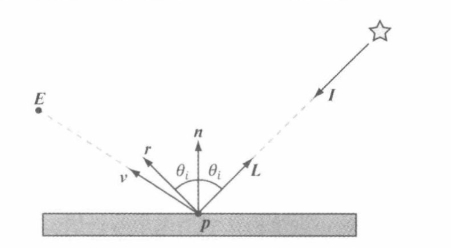
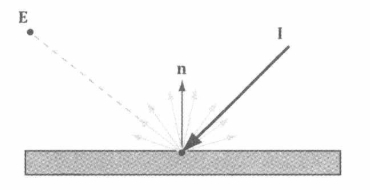
+以上图为例，观察点 p 处沿着单位向量 v 所以顶的视线来进行观察的过程
+
+- 位于表面的点 p 处有法线 n，光线由入射方向 I 照射到点 p
+- **光向量** L 为单位向量，器所指方向与照射到表面上点 p 处入射光线 I 的方向相反
+- 尽管使用入射方向 I 可能更为直观，但是为了进行光照计算，还是采用光向量 L
+- 反射向量 r 是入射光向量 L 关于表面法线 n 的镜像
+- **观察向量** $v = normalize(E-P)$
+- 对于郎伯余弦定律而言，向量 L 用于计算 $L \cdot n = \cos \theta$
+
+已知向量 I，法线 n，如何计算向量 r
+
+![](Image/040.png)
+
+1. 入射向量 I 可以在点 p 处分解为两个向量：一个沿着法线 n 的分量和一个沿着表面的分量
+2. 沿着法线 n 的分量可以计算为  $I \cdot n = |I| * |n| * \cos \theta$ 
+3. 沿着表面的分量是入射向量 I 减去它在法线上的投影，即 $I - I \cdot n$ 
+4. 由于 r 是 I 的反射，r 等于将 I 沿着表面的分量保持不变，而将沿着法线的分量反转 
+5. 所以 r 的向量等于 $(I - I \cdot n) + (I \cdot n) * - 1$，（前面是表面分量，后面是法线分量反转）
+6. 整理公式，得到反射向量 $r = I - 2*(I \cdot n)$
+
+#### 郎伯余弦定律
+
+将光看作是光子的集合，在空间中按特定的方向传播。每个光子都载有能量。光源每秒发出的能量称为**辐射通量**（radiant flux）。单位面积上的辐射通量密度(irradiance，称为辐(射)照度)， 用辐照度来确定表面某区域所接收到的光量（即眼睛感受到的明亮度）
+
+![](Image/041.png)
+
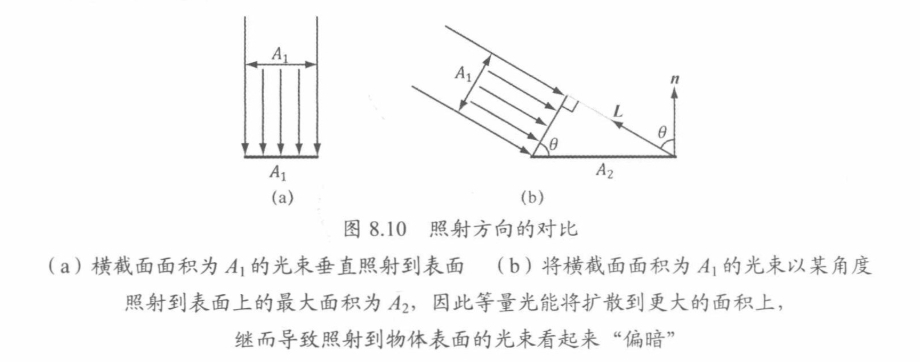
+光线垂直照射到表面的强度要大于以某个角度照射到表面的强度
+
+一小束辐射通量为 p 且截面积为 $A_1$ 的光线，如果光束垂直打向表面则光束照射到表面上的面积为 $A_1$ ，而 $A_1$ 内的辐照度为 $E_1 = P / A_1$
+
+如果旋转光源，使光束以某个入射角度照射到表面上，则光束将覆于表面更大的面积 $A_2$ ，该面积的辐照度为 $E_2 = P / A_2$ 
+
+那么 $A_1$ 和 $A_2$ 的关系就是 $\cos \theta = \frac{A_1}{A_2}$ 等价于 $\frac{1}{A_2} = \frac{\cos \theta}{A_1}$
+
+所以 $E_2 = \frac{p}{A_2} = \frac{p}{A_1}\cos\theta = E_1\cos\theta = E_1(n \cdot L)$
+
+换句话说，面积 $A_2$ 内的辐射度就相当于将受垂直方向光照的面积 $A_1$ 内辐射度按比例 $n \cdot L = \cos \theta$ 进行缩放，这就是**郎伯余弦定律**
+
+![](Image/042.png)
+
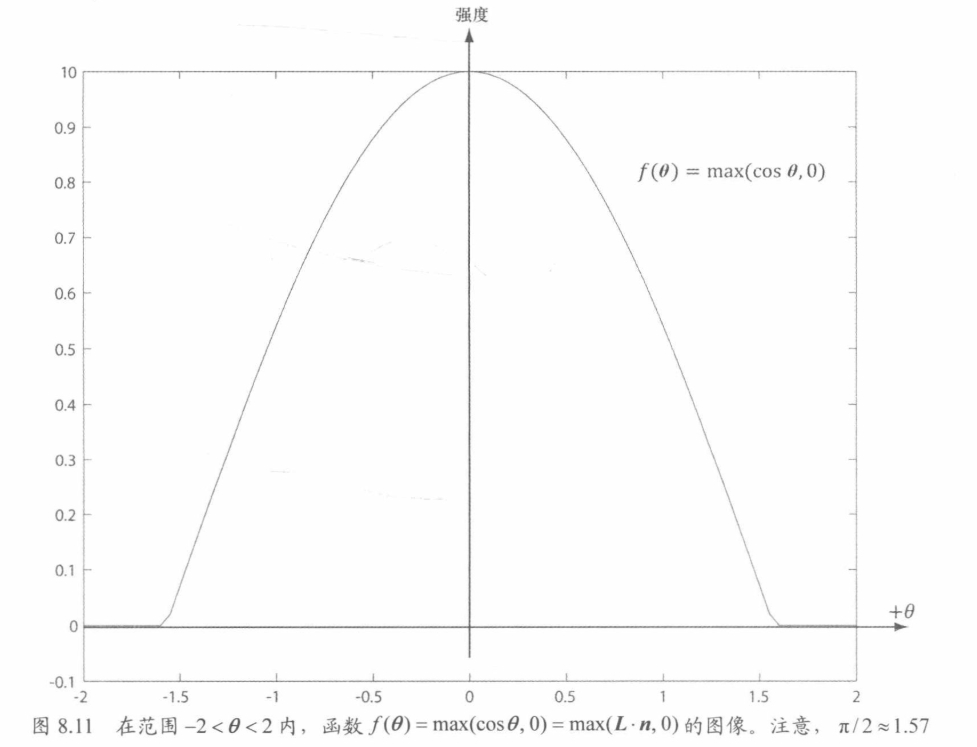
+> $f(\theta) = max(\cos\theta, 0) = max(L \cdot n, 0)$
+
+#### 漫反射光照
+
+![](Image/043.png)
+
+如上图所示，光线照射到表面上的某一点时，一部分光会进入物体的内部，并与表面附近的物质互相作用。这些光会在物体内部四处反弹，其中一部分会被吸收，而余下部分则会向各个方向散射并返回表面，这就是**漫反射**
+
+光的吸收和散射成都与物体的材质密切相关
+
+在所有的光照与材质交互的近似模型中，规定光线会在表面的所有方向上**均匀散射**，因此无论在哪个观察点进行观察，反射光都会进入观察者的眼睛
+
+漫反射光照的计算分为两部分
+
+1. 指定光照颜色以及漫反射反照率(diffuse albedo)
 
 ### 纹理贴图