|
|
@@ -77,6 +77,8 @@ Meadow mapping 是一种用于生成导航网格的方法,它将自由空间
|
|
|
|
|
|
如果区域不是凸多边形,则找到一个凹的角(>180°),尝试将其与多边形内部其他的点连接起来,这个时候会得到两个新的区域,也就是上图的 A 和 B,然后对这两个区域再进行相同的算法,如此一来整个场景就都是凸多边形
|
|
|
|
|
|
+> 也就是递归的**二分法**
|
|
|
+
|
|
|
- 如何判断一个多边形是凸多边形?
|
|
|
|
|
|
检查是否存在大于 180° 的角
|
|
|
@@ -170,11 +172,27 @@ bool isCross(Vector2D a, Vector2D b, Vector2D c, Vector2D d) {
|
|
|
|
|
|
我们先定义什么是**锥形**
|
|
|
|
|
|
-
|
|
|
+
|
|
|
|
|
|
-以上图为例,直线 BA 和 直线 BC 就可以构成一个**锥形**
|
|
|
+以上图为例,直线 (x, x-) 和 直线 (x, x+) 就可以构成一个**锥形**
|
|
|
|
|
|
我们先分类讨论,如果是凸点(小于 180° 角的点),那么对角线在锥形范围内;如果是凹点(大于 180° 角的点),那么对角线在锥形范围外
|
|
|
|
|
|
所以算法的重点在如何判断**直线在锥形范围内**
|
|
|
|
|
|
+其实也很简单,如果点在锥形范围内,那么该点在 (x-, x) 线段左边,并且在 (x, x+) 线段左边
|
|
|
+
|
|
|
+综合以上几种算法,我们可以检测对**角线是否与非临边相交**和**对角线是否在锥形内部**
|
|
|
+
|
|
|
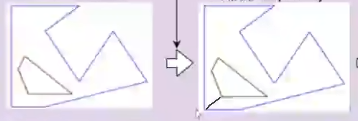
+如果多边形内部存在 hole (洞),解决方法其实也很简单,将内部洞与外围点连接,将带空洞的多边形变为简单多边形,当然这个内部洞与外围的连接点也必须是互相**可见**的
|
|
|
+
|
|
|
+
|
|
|
+
|
|
|
+上图连接的一根线,将带空洞的多边形变成了下图这种简单多边形,下图稍微夸张了一点分割部分,主要是为了强调这根线的作用
|
|
|
+
|
|
|
+
|
|
|
+
|
|
|
+在 `Recast Navigation` 中,划分凸多边形使用的是耳切法(`Ear Clipping`),`Meadow Mapping` 划分凸多边形则使用的是二分法。耳切法使用更加聪明的方式,使得每个切出来的区域都是单独的三角形,避免 `Meadow Mapping` 递归调用的额外开销
|
|
|
+
|
|
|
+`Recast Navigation` 是一种基于耳切法的划分算法,它的基本思想是从一个凸多边形的任意一个顶点开始,判断该顶点是否是一个耳朵,即该顶点的内角小于 180°,并且以该顶点为顶点的三角形不包含其他顶点。如果是耳朵,那么就将该顶点和相邻的两个顶点组成一个三角形,从多边形中切除该耳朵,否则就跳过该顶点,继续检查下一个顶点。重复上述过程,直到多边形被切割成若干个三角形为止。然后对每个三角形进行合并,使其满足最大顶点数的限制,得到最终的凸多边形集合。这种算法的优点是划分后的多边形的角度较大,有利于寻路效率,缺点是划分后的多边形数量较多,占用空间较大
|
|
|
+
|