添加辐射度量学的简单介绍

图形学/图形学.md

@@ -2320,7 +2320,88 @@ $t_{quit} = max(t_{x_{max}}, t_{y_{max}}, t_{z_{max}})$
 
 这样子可以保证一个物体只会在记录一个包围盒中(**包围盒可以重叠**)，并且包围盒的范围更好计算(取所有物体点坐标的最小x、最小y、最大x、最大y就是包围盒的范围)
 
-但是 BVH 引入了一个新问题那就是 **包围盒可以相交**，那么如何进行空间划分能够让包围盒重叠尽可能少？
+但是 BVH 引入了一个新问题那就是 **包围盒可以相交**，那么如何进行空间划分才算好？
+
+- 分割法1：可以参考上面空间划分的方法，每次每次划分不同的轴
+- 分割法2：每次沿着最长的轴分割成两半
+- 分割法3：确定沿着某个轴分割，那么将所有物体的重心沿着轴线排序，从序号中间的物体进行分割，比如n个物体就从排序后序号为n/2个物体开始分割，其实用不到排序这种 O(n*lgn)的算法，可以使用类快排解法 时间复杂度O(n)
+
+物体动了、场景更新了，就得重新计算新的BVH
+
+BVH的数据结构
+
+- 非叶子节点：存储包围盒信息，左右节点指针
+- 叶子节点：存储包围盒信息，具体物体数组
+
+## 辐射度量学 Basic Radiometry
+
+辐射度量学是基于物理光照的基础，物理上准确定义光照的方法
+
+精确描述物体表面与光的作用、光源、材质、光线的传播方法
+
+定义了一系列方法、范围，给光在空间中的属性，基于几何光学(直线传播，没有波动性)，定义光照的若干属性
+
+| 专业名词 | 中文翻译 |
+| --- | --- |
+| Radiant Flux | 辐射通量 | 
+| Radiant Intensity | 辐射强度 | 
+| Irradiance | 辐\[射]照度 |
+| Radiance | 辐\[射]亮度 |
+
+上面的 `Whitted-Style` 光线追踪很多都是相似
+
+`Radiant Energy` 辐射能量 单位是 J(`Joule` 焦耳)
+
+`Radiant Flux` 又称 `Power` 指的是 单位时间的能量 也就是**功率** 单位是 W(`Watt` 瓦特)
+
+光学中描述物体的功率，单位是 lm(`lumen` 流明)，表示有多亮
+
+> 流明一般在购买投影仪的时候作为参数进行购买，数值越大越亮
+
+![](./Image/132.png)
+
+- `Radiant Intensity` 
+
+光源向四面八方都有可能辐射能量，定义的方向性的能量相关
+
+定义：单位立体角的功率 
+
+公式：$ I(\omega) \equiv \frac{\mathrm{d} \Phi}{\mathrm{d} \omega} $
+
+$$
+\left[\frac{\mathrm{W}}{\mathrm{sr}}\right]
+\left[\frac{\mathrm{lm}}{\mathrm{sr}}=\mathrm{cd}=\text { candela }\right]
+$$
+
+$ sr $ 是立体角的单位, $ cd $ 是 `Radiant Intensity`的单位
+
+至于立体角
+
+![](./Image/133.png)
+
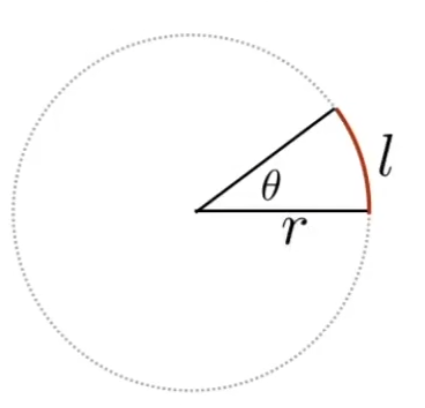
+在二维平面上， $ \theta=\frac{l}{r} $ 
+
+![](./Image/134.png)
+
+**立体角**就是上面的公式推广到三维平面上 $ \Omega=\frac{A}{r^{2}} $ 
+
+![](./Image/135.png)
+
+$$
+\begin{aligned}
+\Phi & =\int_{S^{2}} I \mathrm{~d} \omega & =4 \pi I
+\end{aligned}
+$$
+
+通过上面的式子，可以得出 如果点光源向各个方向均匀的发出光线，那么任意方向上的 `Radiant Intensity` 就是 $ I=\frac{\Phi}{4 \pi} $
+
+以白炽灯为例，如果白炽灯为815lm，那么它的 `Radiant Intensity` 就是 $ 815 lumens / 4 \pi sr = 65 candelas $
+
+- `Irradiance` 物体表面接收到多少光的能林
+
+
+
+- `Radiance` 光在传播中度量能量