|
|
@@ -1,7 +1,7 @@
|
|
|
<!--
|
|
|
* @Author: your name
|
|
|
* @Date: 2021-10-01 11:33:27
|
|
|
- * @LastEditTime: 2022-02-23 01:17:38
|
|
|
+ * @LastEditTime: 2022-02-24 00:06:14
|
|
|
* @LastEditors: Please set LastEditors
|
|
|
* @Description: In User Settings Edit
|
|
|
* @FilePath: D:\MarkdownLog\图形学.md
|
|
|
@@ -1153,12 +1153,12 @@ shading,引入物体的明暗的不同,颜色的不同,**对不同的物
|
|
|
- 颜色color
|
|
|
- 光的亮度 shininess
|
|
|
|
|
|
+
|
|
|
+
|
|
|
> 所有的方向都是单位向量,只表示方向
|
|
|
|
|
|
#### 漫反射
|
|
|
|
|
|
-
|
|
|
-
|
|
|
> 暂且只讨论某一个点的着色,也就是只考虑光照的方向,而不考虑照向这个点的光是不是被挡住了
|
|
|
|
|
|

|
|
|
@@ -1198,6 +1198,139 @@ $$
|
|
|
|
|
|
通过定义$k_d$颜色系数,可以定义该物体整体上的明暗
|
|
|
|
|
|
+#### 高光
|
|
|
+
|
|
|
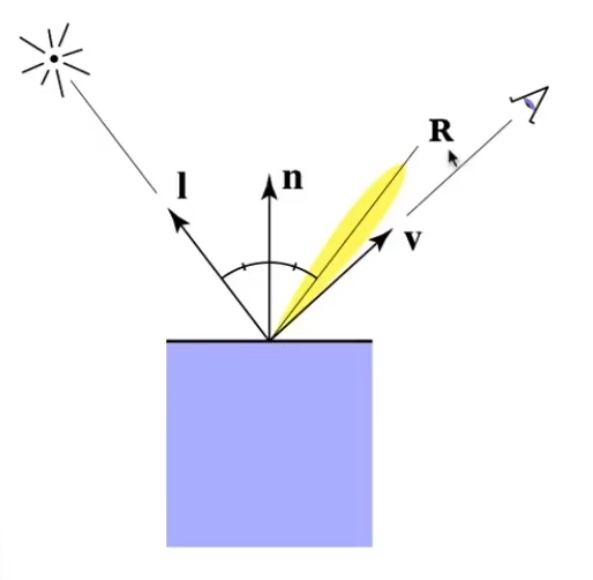
+高光:物体、平面比较光滑,所以反射光线的方向都接近镜面反射的方向
|
|
|
+
|
|
|
+
|
|
|
+
|
|
|
+图中R表示镜面反射的方向,黄色部分表示高光反射的区域,v表示观察方向
|
|
|
+
|
|
|
+所以当观察方向与镜面反射方向相近的时候,可以看到物体的高光
|
|
|
+
|
|
|
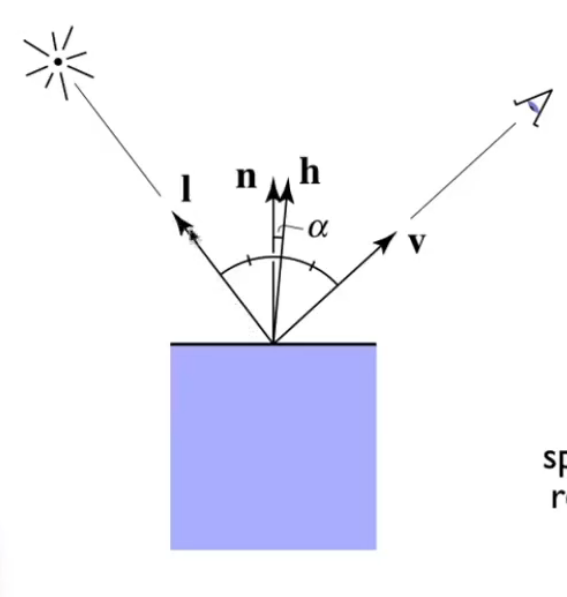
+在Blinn-Phong模型中,观察方向与镜面反射方向接近的时候,说明了平面的法线方向和 **半程向量(half vector)** 接近
|
|
|
+
|
|
|
+
|
|
|
+
|
|
|
+$$
|
|
|
+半程向量:\vec{h} = bisector(\vec{v}, \vec{l}) = \frac{\vec{v} + \vec{l}}{\lVert \vec{v} + \vec{l} \rVert}
|
|
|
+\\
|
|
|
+L_s = k_s(I / r^2)max(0, \cos \alpha)^p
|
|
|
+\Rightarrow
|
|
|
+k_s(I / r^2)max(0, n \cdot h)^p
|
|
|
+$$
|
|
|
+
|
|
|
+- 高光的计算公式 $L_s$
|
|
|
+ - $k_s$高光系数,颜色之类的,跟漫反射系数类似
|
|
|
+ - $(I / r^2)$跟漫反射中的一样,高达此处的光的强度
|
|
|
+ - $max(0, \vec{n} \cdot \vec{h})^p$根据观察角度能得到多少光
|
|
|
+
|
|
|
+1. 为啥使用半程向量:半程向量的计算比直接计算光的镜面反射向量简单
|
|
|
+2. $\cos \alpha$,在$0~\pi$是单调递减的,复合这里$\alpha$越小高光越多的情况
|
|
|
+3. 不考虑从$\cos \alpha$为负数的情况,此时光从下面照射
|
|
|
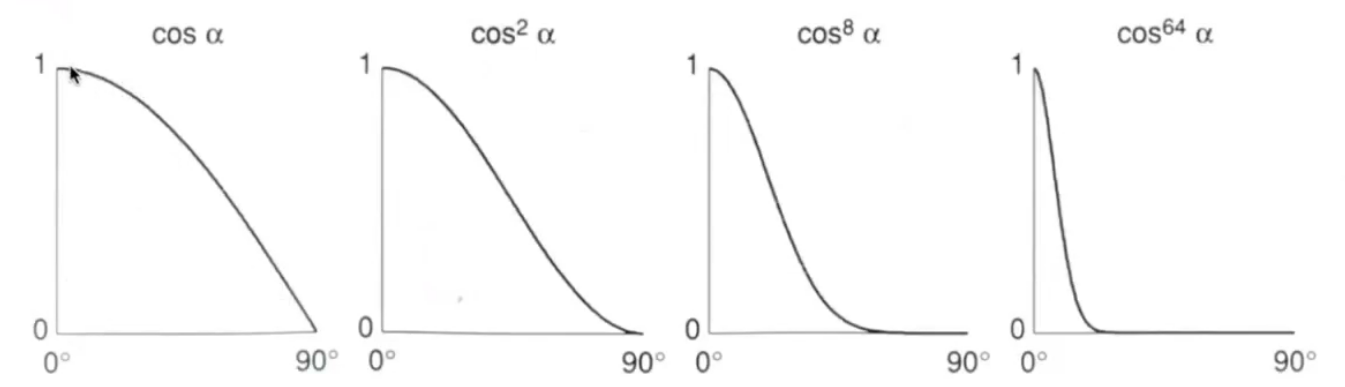
+4. $max(0, \vec{n} \cdot \vec{h})^p$中指数p的作用如图下所示,通过参数p可以指定高光范围的大小(p越大,高光范围越小,对应下图p越大,数据变小越快,一般100~200)
|
|
|
+
|
|
|
+
|
|
|
+
|
|
|
+
|
|
|
+
|
|
|
+从上到下 高光系数 $k_s$ 逐渐变大,可以发现越来越亮;从左到右 指数p 逐渐变大,高光范围逐渐变小
|
|
|
+
|
|
|
+#### 环境光照
|
|
|
+
|
|
|
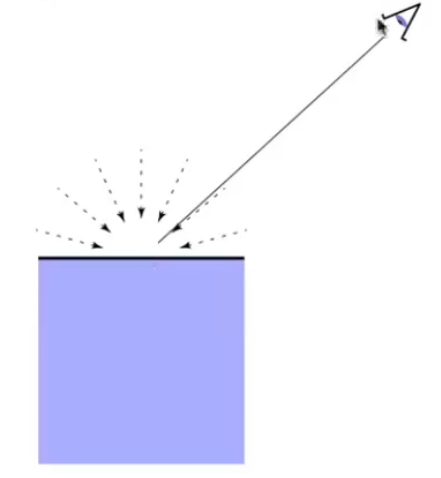
+对于处于物体背面的平面不一定就是黑色的,因为有环境光的存在,虽然不会被光线直接照射到,但是会被其他平面的漫反射光照到
|
|
|
+
|
|
|
+在Blinn-Phong模型中,直接大胆假设:任何一个点接收到来自环境的光永远是相同的
|
|
|
+
|
|
|
+
|
|
|
+
|
|
|
+从图中可以发现,环境光与光照角度无光,与观察角度无关(每个角度观察都一样),因此环境光是一个**常数**,即是某一种颜色(比如说一个物体,在任何地方都有一个固定的颜色)
|
|
|
+
|
|
|
+环境光保证一个物体不是全是黑色的,在高光、漫反射计算完之后叠加环境光,提升一个亮度
|
|
|
+
|
|
|
+$$
|
|
|
+L_a = k_aI_a
|
|
|
+$$
|
|
|
+
|
|
|
+- 环境光 $L_a$
|
|
|
+ - $K_a$ 环境光照系数
|
|
|
+
|
|
|
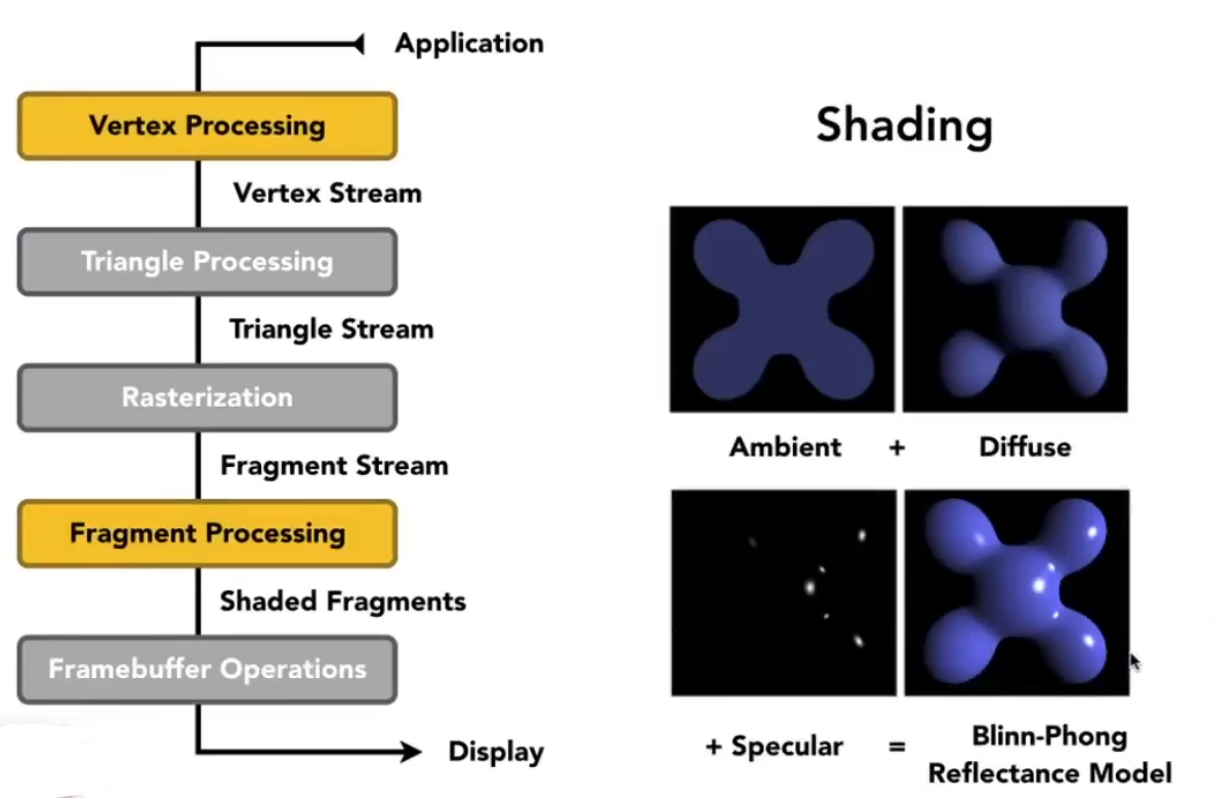
+#### 累加
|
|
|
+
|
|
|
+
|
|
|
+
|
|
|
+> Ambient 环境光、Diffuse 漫反射、Specular 高光
|
|
|
+
|
|
|
+$$
|
|
|
+L = L_a + L_d + L_s=
|
|
|
+k_aI_a + k_d(I / r^2)max(0, \vec{n} \cdot \vec{l}) + k_s(I/r^2)max(0, \vec{n} \cdot \vec{h})^p
|
|
|
+$$
|
|
|
+
|
|
|
+### 着色频率
|
|
|
+
|
|
|
+
|
|
|
+
|
|
|
+三个球的几何表示在空间中是一样的,但是表现出来的结果却不相同
|
|
|
+
|
|
|
+着色频率:要把着色应用在哪些点上
|
|
|
+
|
|
|
+比如图中最左边的球,就是把着色应用在一个**面**上,即一个平面有一个固定发现,求出的结果被应用在整个面上(**Flat Shading**)
|
|
|
+
|
|
|
+比如图中中间的球,一个平面有四个**顶点**,算出每个顶点对应的法线,那么每个顶点都有自己的着色效果,通过差值插值运算,让平面中有较为平滑的过度(**Gouraud Shading**)
|
|
|
+
|
|
|
+比如图中最右边的球,就是把着色应用在每一个**像素上**(**Phong Shading**)
|
|
|
+
|
|
|
+> **Phong Shading**并不是**Blinn-Phong**,前者是着色频率,后者是着色模型
|
|
|
+
|
|
|
+
|
|
|
+
|
|
|
+图中每一行的模型相同,从上网下模型精细度增加
|
|
|
+
|
|
|
+从图中可以观察到,当几何体足够精细的情况下,就可以使用相对简单的**Flat Shading**着色频率,得到的结果其实也不差
|
|
|
+
|
|
|
+> 当面足够精细的时候,就不一定要使用**Gouraud Shading** 或者 **Phong Shading**
|
|
|
+
|
|
|
+所以运用何种着色频率,需要根据具体几何体的情况而定,而不是一味的选择像素频率**Phong Shading**
|
|
|
+
|
|
|
+### 计算法线
|
|
|
+
|
|
|
+法线:垂直于平面的向量
|
|
|
+
|
|
|
+**顶点的法线**:顶点相邻面的法线的平均值
|
|
|
+
|
|
|
+
|
|
|
+
|
|
|
+$$
|
|
|
+N_v = \frac{\sum _iN_i}{\lVert \sum _iN_i \rVert}
|
|
|
+$$
|
|
|
+
|
|
|
+**逐像素法线**:通过重心坐标
|
|
|
+
|
|
|
+### 图形管线、实时渲染管线
|
|
|
+
|
|
|
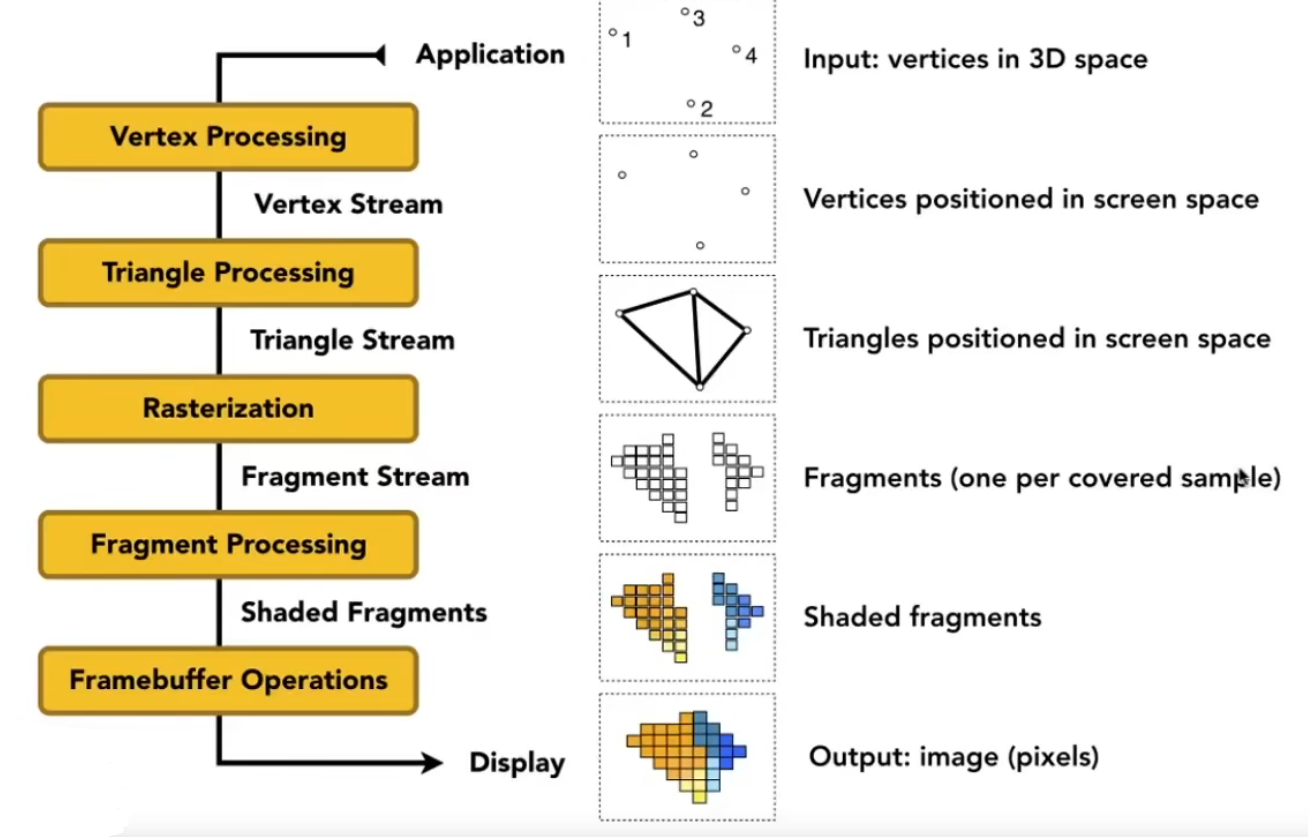
+如何从场景到一张图?
|
|
|
+
|
|
|
+管线其实就是表示一系列不同的操作
|
|
|
+
|
|
|
+
|
|
|
+
|
|
|
+1. 三维空间的点投影到平面上
|
|
|
+2. 模型的点形成三角形
|
|
|
+3. 光栅化,进行离散操作
|
|
|
+4. 着色
|
|
|
+5. 渲染到屏幕
|
|
|
+
|
|
|
+
|
|
|
+
|
|
|
+这里**shading**既有可能发生在**Vertex Processing**也有可能发生**Fragment Processing**,因为渲染频率的问题,因为渲染频率既可能是顶点频率,也可能是像素频率,而这就影响了渲染管线的处理顺序
|
|
|
+
|
|
|
+Shader控制顶点管线(**Vertex Processing**)和着色管线如何运作(**Fragment Processing**)
|
|
|
+
|
|
|
+现在GPU允许通过编程的方式,处理顶点、像素的着色操作,通过shader的方式
|
|
|
+
|
|
|
+- OpenGL: GLSL语言
|
|
|
+- DirectX: HLSL语言
|
|
|
+
|
|
|
# 几何
|
|
|
|
|
|
如何表示光滑的曲线、曲面、将简单曲面通过细分的方法得到复杂曲面、形状发生变化时面如何变化、如何保持物体的拓扑结构…
|