|
|
@@ -1598,10 +1598,167 @@ void main()
|
|
|
|
|
|
#### 延迟渲染和前向渲染结合
|
|
|
|
|
|
-如果想要渲染光源在场景中,使用延迟渲染是做不到的
|
|
|
+如果想要渲染光源物体在场景中,使用延迟渲染是做不到的
|
|
|
|
|
|
-- G-Buffer 中只存储了场景物体的几何信息,不包含光源本身的几何信息
|
|
|
-- 光源立方体需要自己的深度计算,与场景深度缓冲冲突
|
|
|
-- 延迟渲染的光照阶段输出的是光照结果,而不是光源的几何表示
|
|
|
+- G-Buffer 中只存储了场景物体的几何信息,不包含光源物体本身的几何信息
|
|
|
+- 光源立方体不接受光照,不应该参与阴影计算或遮挡关系
|
|
|
+
|
|
|
+
|
|
|
+
|
|
|
+为了确保光源立方体的深度信息正确,在延迟渲染计算完 G-Buffer 和 光照计算 之后,会复制 **深度信息** 到缓冲区中,再通过前向渲染计算**光源**和**透明物体**
|
|
|
+
|
|
|
+```cpp
|
|
|
+// 渲染伪代码
|
|
|
+void FDeferredShadingSceneRenderer::Render()
|
|
|
+{
|
|
|
+ // 基础通道:填充GBuffer
|
|
|
+ RenderBasePass();
|
|
|
+
|
|
|
+ // 光照计算
|
|
|
+ RenderLights();
|
|
|
+
|
|
|
+ // 复制深度到主缓冲区
|
|
|
+ CopySceneDepth();
|
|
|
+
|
|
|
+ // 渲染透明物体和光源可视化
|
|
|
+ RenderTranslucency();
|
|
|
+ RenderLightVisualizations(); // 光源立方体在这里渲染
|
|
|
+}
|
|
|
+```
|
|
|
+
|
|
|
+#### 光体积(Light Volumes)
|
|
|
+
|
|
|
+#### 延迟光照(Deferred Lighting)
|
|
|
+
|
|
|
+#### 切片式延迟着色法(Tile_based Deferred Shading)
|
|
|
+
|
|
|
+### 屏幕环境光遮罩(SSAO, Screen-Space Ambient Occlusion)
|
|
|
+
|
|
|
+
|
|
|
+
|
|
|
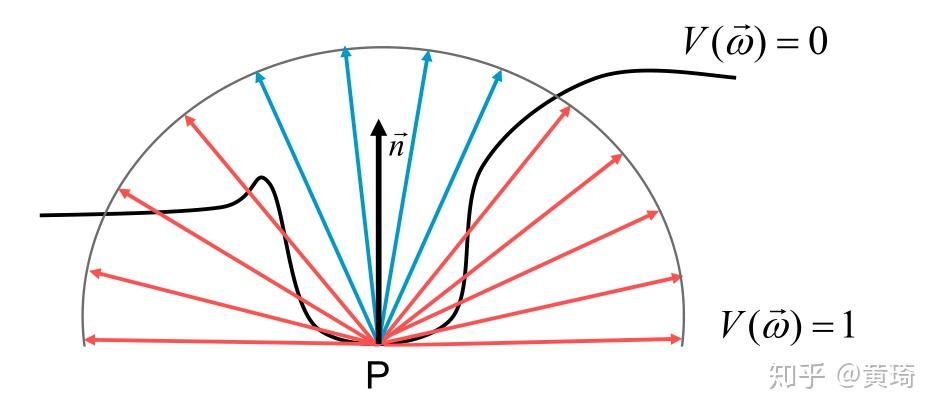
+有一种间接光照的模拟叫做**环境光遮蔽**(`Ambient Occlusion`),它的原理是通过将褶皱、孔洞和非常靠近的墙面变暗的方法近似模拟出间接光照
|
|
|
+
|
|
|
+AO(Ambient Occlution) 是通过在场景中的点上产生一个标量值来描述由这点向各个方向射出的光线被遮挡的概率 , 这个标量值可以用来产生全局的遮挡效果 , 并为用户提供关于场景中物体之间的位置关系和物体表面的起伏情况的重要视觉信息
|
|
|
+
|
|
|
+
|
|
|
+
|
|
|
+> 计算 P 点向各个方向射出的光线被遮挡的概率,就是该点的标量值
|
|
|
+
|
|
|
+SSAO 的基本思想是:表面上某点接收到的环境光量取决于其周围几何体对该点的遮挡程度。在屏幕空间中,算法通过采样当前像素周围点的深度信息,估算该点被周围几何体遮挡的程度
|
|
|
+
|
|
|
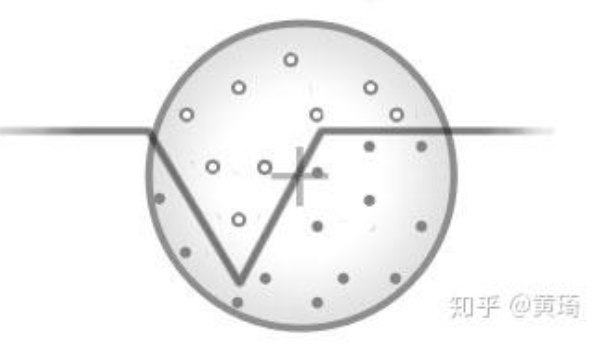
+| 没有法线信息 | 有法线信息 |
|
|
|
+| --- | --- |
|
|
|
+|  |  |
|
|
|
+
|
|
|
+- 如果没有法线信息,则以目标点为球心,R为半径的球体内,进行随机若干三维采样
|
|
|
+- 如果有法线信息,则以目标点为球心,R为半径的半球体内,进行随机若干三位采样
|
|
|
+
|
|
|
+对于每个采样点,计算其对当前点的遮挡贡献
|
|
|
+
|
|
|
+```cpp
|
|
|
+float occlusion = 0.0;
|
|
|
+const int numSamples = 16;
|
|
|
+
|
|
|
+for(int i = 0; i < numSamples; i++) {
|
|
|
+ // 生成采样点位置
|
|
|
+ vec3 sampleOffset = randomHemispherePoint(texCoords, normal);
|
|
|
+ vec3 samplePos = viewPos + sampleOffset;
|
|
|
+
|
|
|
+ // 将采样点投影回屏幕空间
|
|
|
+ vec4 sampleClip = projection * vec4(samplePos, 1.0);
|
|
|
+ sampleClip.xyz /= sampleClip.w; // 透视除法
|
|
|
+ vec2 sampleUV = sampleClip.xy * 0.5 + 0.5;
|
|
|
+
|
|
|
+ // 获取采样点处的实际深度
|
|
|
+ float sampleDepth = texture(gDepth, sampleUV).r;
|
|
|
+
|
|
|
+ // 重建采样点处的实际观察空间位置
|
|
|
+ vec4 actualPos = invProjection * vec4(sampleClip.xy, sampleDepth * 2.0 - 1.0, 1.0);
|
|
|
+ actualPos /= actualPos.w;
|
|
|
+
|
|
|
+ // 计算遮挡程度
|
|
|
+ float rangeCheck = smoothstep(0.0, 1.0, radius / abs(viewPos.z - actualPos.z));
|
|
|
+ float sampleOcclusion = max(0.0, actualPos.z - samplePos.z) * rangeCheck;
|
|
|
+
|
|
|
+ occlusion += sampleOcclusion;
|
|
|
+}
|
|
|
+
|
|
|
+occlusion = 1.0 - (occlusion / numSamples);
|
|
|
+```
|
|
|
+
|
|
|
+原始 SSAO 结果通常包括噪声,所以需要后处理,比如模糊滤波
|
|
|
+
|
|
|
+```cpp
|
|
|
+// 双边模糊滤波
|
|
|
+vec3 blurSSAO(vec2 uv) {
|
|
|
+ vec3 result = vec3(0.0);
|
|
|
+ float totalWeight = 0.0;
|
|
|
+ vec3 centerNormal = texture(gNormal, uv).rgb;
|
|
|
+ float centerDepth = texture(gDepth, uv).r;
|
|
|
+
|
|
|
+ for(int x = -2; x <= 2; x++) {
|
|
|
+ for(int y = -2; y <= 2; y++) {
|
|
|
+ vec2 offset = vec2(x, y) * pixelSize;
|
|
|
+ vec2 sampleUV = uv + offset;
|
|
|
+
|
|
|
+ vec3 sampleNormal = texture(gNormal, sampleUV).rgb;
|
|
|
+ float sampleDepth = texture(gDepth, sampleUV).r;
|
|
|
+ float sampleOcc = texture(ssaoRaw, sampleUV).r;
|
|
|
+
|
|
|
+ // 深度和法线相似度权重
|
|
|
+ float depthDiff = abs(centerDepth - sampleDepth);
|
|
|
+ float normalDiff = dot(centerNormal, sampleNormal);
|
|
|
+
|
|
|
+ float depthWeight = exp(-depthDiff * depthScale);
|
|
|
+ float normalWeight = max(0.0, normalDiff);
|
|
|
+
|
|
|
+ float weight = depthWeight * normalWeight;
|
|
|
+
|
|
|
+ result += sampleOcc * weight;
|
|
|
+ totalWeight += weight;
|
|
|
+ }
|
|
|
+ }
|
|
|
+
|
|
|
+ return result / totalWeight;
|
|
|
+}
|
|
|
+```
|
|
|
+
|
|
|
+## PBR
|
|
|
+
|
|
|
+`Physically-Based Render` 基于物理的渲染,简称 `PBR`,它指的是一些在不同程度上都基于与现实世界的物理原理更相符的基本理论所构成的渲染技术的集合。核心目标是让物体表面的材质(金属、塑料、木头、皮肤等)在光照下的表现符合物理世界的规律
|
|
|
+
|
|
|
+通常来说 `PBR` 渲染的结果比使用 `Phong` 或者 `Blinn-Phong` 模型渲染的效果更加真实
|
|
|
+
|
|
|
+`PBR` 的核心思想
|
|
|
+
|
|
|
+1. 能量守恒,物体表面反射的光线(漫反射和镜面反射)总量不能超过入射光线的总量
|
|
|
+2. 微表面理论,将物体表面视为无数微小的、方向随机的镜面组面组成。材质的粗糙度决定了这些微表面的排列是光滑(高光集中)还是粗糙(高光分散)
|
|
|
+3. 应用基于物理的 `BRDF`
|
|
|
+ - `BRDF` 是一个数学函数,描述了光线如何在一个特定的表面点上发生反射
|
|
|
+ - 输入:入射光方向 (ωᵢ)、出射光方向 (ωₒ)、表面位置、波长。
|
|
|
+ - 输出:反射率比例。即,对于从ωᵢ方向入射的一束光,有多少比例的能量被反射到ωₒ方向上
|
|
|
+4. 菲涅尔效应: 光线以不同角度照射到表面时,反射和折射的比例会发生变化(掠射角时反射更强)
|
|
|
+5. 使用物理可测量的参数,基础反色率、粗糙度、金属度等
|
|
|
+6. 光线路劲的可逆性,交换入射光和出射光方向, `BRDF` 值不变
|
|
|
+
|
|
|
+### 微平面模型
|
|
|
+
|
|
|
+所有的 `PBR` 技术都基于微平面理论。这项理论认为,达到微观尺度之后任何平面都可以用被称为微平面(`Microfacets`)的细小镜面来进行描绘。根据平面粗糙程度的不同,这些细小镜面的取向排列可以相当不一致
|
|
|
+
|
|
|
+产生的效果就是:一个平面越是粗糙,这个平面上的微平面的排列就越混乱。这些微小镜面这样无序取向排列的影响就是,当我们特指镜面光/镜面反射时,入射光线更趋向于向完全不同的方向发散(Scatter)开来,进而产生出分布范围更广泛的镜面反射。而与之相反的是,对于一个光滑的平面,光线大体上会更趋向于向同一个方向反射,造成更小更锐利的反射
|
|
|
+
|
|
|
+
|
|
|
+
|
|
|
+在微观尺度下,没有任何平面是完全光滑的。然而由于这些微平面已经微小到无法逐像素地继续对其进行区分,因此我们假设一个粗糙度(Roughness)参数,然后用统计学的方法来估计微平面的粗糙程度。我们可以基于一个平面的粗糙度来计算出众多微平面中,朝向方向沿着某个向量 `h` 方向的比例。这个向量 `h` 便是位于光线向量 `l` 和视线向量 `v` 之间的半程向量(`Halfway Vector`)
|
|
|
+
|
|
|
+微平面的朝向方向与半程向量的方向越是一致,镜面反射的效果就越是强烈越是锐利。通过使用一个介于0到1之间的粗糙度参数,我们就能概略地估算微平面的取向情况
|
|
|
+
|
|
|
+
|
|
|
+
|
|
|
+### 能量守恒
|
|
|
+
|
|
|
+出射光线的能量永远不能超过入射光线的能量(发光面除外)
|
|
|
+
|
|
|
+根据前面的图片可以看到,粗糙度越高,反射区域越大,但是亮度越暗;粗糙度越高,反射区域越小,但是亮度越亮
|
|
|
|
|
|
|