Projection

图形学/图形学.md

@@ -1,13 +1,14 @@
 <!--
  * @Author: your name
  * @Date: 2021-10-01 11:33:27
- * @LastEditTime: 2022-02-19 20:16:03
+ * @LastEditTime: 2022-02-20 18:56:59
  * @LastEditors: Please set LastEditors
  * @Description: In User Settings Edit
  * @FilePath: D:\MarkdownLog\图形学.md
--->
 
-<script type="text/javascript" src="http://cdn.mathjax.org/mathjax/latest/MathJax.js?config=default"></script>
+https://latex.codecogs.com/svg.latex?\vec{A}=(^{x}_{y})\\\vec{A}^T=(x,y)\\\lVert\vec{A}=\sqrt{x^2+y^2}\rVert\
+
+-->
 
 为什么要学习计算机图形学？——计算机图形学就是厉害
 
@@ -129,8 +130,7 @@ k *
     x & a \\ 
     y & b \\
     z & c \\
-\end{pmatrix}
- = 
+\end{pmatrix} = 
 \begin{pmatrix}
     k*x & k*a \\ 
     k*y & k*b \\
@@ -149,13 +149,11 @@ $$
     x_1 & a_1 \\ 
     y_1 & b_1 \\
     z_1 & c_1 \\
-\end{pmatrix}
-*
+\end{pmatrix}*
 \begin{pmatrix}
     x_2 & a_2 & q_2 & e_2 \\ 
     y_2 & b_2 & w_2 & r_2 \\
-\end{pmatrix}
-=
+\end{pmatrix}=
 \begin{pmatrix}
     x_1 * x_2 + a_1 * y_2 & x_1 * a_2 + a_1 * b_2 & x_1 * q_2 + a_1 * w_2 & x_1 * e_2 + a_1 * r_2 \\ 
     y_1 * x_2 + b_1 * y_2 & y_1 * a_2 + b_1 * b_2 & y_1 * q_2 + b_1 * w_2 & y_1 * e_2 + b_1 * r_2 +\\
@@ -175,13 +173,11 @@ $$
 \begin{bmatrix}
     -1 & 0 \\
     0 & 1
-\end{bmatrix} 
-*
+\end{bmatrix} *
 \begin{bmatrix}
     x\\
     y
-\end{bmatrix}
-=
+\end{bmatrix}=
 \begin{bmatrix}
     -x \\
     y
@@ -228,8 +224,7 @@ $$
 \end{bmatrix} 
 \begin{bmatrix}
     x_b \\ y_b \\ z_b
-\end{bmatrix}
-= \left( x_a*x_b + y_a*y_b + z_a*z_b \right)
+\end{bmatrix}= \left( x_a*x_b + y_a*y_b + z_a*z_b \right)
 $$
 
 向量的叉乘转成矩阵运算
@@ -262,8 +257,7 @@ y^` = sy\\
 \Rightarrow \\
 \begin{bmatrix}
     x^` \\ y^`
-\end{bmatrix}
-= 
+\end{bmatrix}= 
 \begin{bmatrix}
     s & 0 \\
     0 & s 
@@ -283,8 +277,7 @@ y^` = y\\
 \Rightarrow \\
 \begin{bmatrix}
     x^` \\ y^`
-\end{bmatrix}
-= 
+\end{bmatrix}= 
 \begin{bmatrix}
     -1 & 0 \\
     0 & 1 
@@ -304,8 +297,7 @@ y^` = y\\
 \Rightarrow \\
 \begin{bmatrix}
     x^` \\ y^`
-\end{bmatrix}
-= 
+\end{bmatrix}= 
 \begin{bmatrix}
     1 & a \\
     0 & 1 
@@ -351,16 +343,14 @@ $$
 $$
 \begin{bmatrix}
     x^` \\ y ^ `
-\end{bmatrix}
-=
+\end{bmatrix}=
 \begin{bmatrix}
     1 & 0 \\
     0 & 1 
 \end{bmatrix}
 \begin{bmatrix}
     x \\ y
-\end{bmatrix}
-+
+\end{bmatrix}+
 \begin{bmatrix}
     t_x \\ t_y
 \end{bmatrix}
@@ -373,8 +363,7 @@ $$
 $$
 \begin{bmatrix}
     x^` \\ y ^ ` \\ 1
-\end{bmatrix}
-=
+\end{bmatrix}=
 \begin{bmatrix}
     1 & 0 & t_x \\
     0 & 1 & t_y \\
@@ -382,8 +371,7 @@ $$
 \end{bmatrix}
 \begin{bmatrix}
     x \\ y \\ 1
-\end{bmatrix}
-=
+\end{bmatrix}=
 \begin{bmatrix}
     x + t_x \\ y + t_y \\ 1
 \end{bmatrix}
@@ -409,16 +397,14 @@ $$
 $$
 A = \begin{pmatrix}
     x \\ y \\ w
-\end{pmatrix}
-=
+\end{pmatrix}=
 \begin{pmatrix}
     x / w \\ y / w \\ 1
 \end{pmatrix}
 \\
 B = \begin{pmatrix}
     a \\ b \\ c
-\end{pmatrix}
-=
+\end{pmatrix}=
 \begin{pmatrix}
     a / c \\ b / c \\ 1
 \end{pmatrix}
@@ -426,8 +412,7 @@ B = \begin{pmatrix}
 A + B = 
 \begin{pmatrix}
     x/w + a/c \\ y/w + b/c \\ 2
-\end{pmatrix}
-=
+\end{pmatrix}=
 \begin{pmatrix}
     \frac{x}{2w} + \frac{a}{2c} \\
     \frac{y}{2w} + \frac{b}{2c} \\
@@ -463,6 +448,14 @@ T(t_x, t_y) =
 \end{pmatrix}
 $$
 
+### 逆变换
+
+![逆变换](./Image/9.png)
+
+逆变换就是把之前的操作反向来一次，对应的就是矩阵中的逆矩阵 
+
+
+
 ### 组合变换
 
 - 图1
@@ -480,8 +473,7 @@ $$
 $$
 T_{(1， 0)} \cdot R_{45} \cdot \begin{bmatrix}
     x \\ y \\ 1
-\end{bmatrix}
-= 
+\end{bmatrix}= 
 \begin{bmatrix}
     1 & 0 & 1 \\
     0 & 1 & 0 \\
@@ -518,19 +510,19 @@ $$
 
 ### 三位空间的变换
 
+三维与二维无非就是多了一个维度，其他的变换相似，原理相同
+
 point : $\begin{pmatrix}
-    x \\ y \\ z \\ 1
-\end{pmatrix}$  
+    x & y & z & 1
+\end{pmatrix}^T$  
 vector : $\begin{pmatrix}
-    x \\ y \\ z \\ 0
-\end{pmatrix}$
+    x & y & z & 0
+\end{pmatrix}^T$
 
 $$
-
 \begin{pmatrix}
     x^` \\ y^1 \\ z^` \\ 1
-\end{pmatrix}
-=
+\end{pmatrix}=
 \begin{pmatrix}
     a & b & c & t_x \\
     d & e & f & t_y \\
@@ -540,15 +532,315 @@ $$
 \begin{pmatrix}
     x \\ y \\ z \\ 1
 \end{pmatrix}
+\\
+Scale \Longrightarrow
+S(s_x, s_y, s_z) =
+\begin{pmatrix}
+    s_x & 0 & 0 & 0 \\
+    0 & s_y & 0 & 0 \\
+    0 & 0 & s_z & 0 \\
+    0 & 0 & 0 & 1
+\end{pmatrix}
+\\
+Translation \Longrightarrow
+T(t_x, t_y, t_z) =
+\begin{pmatrix}
+    1 & 0 & 0 & t_x \\
+    0 & 1 & 0 & t_y \\
+    0 & 0 & 1 & t_z \\
+    0 & 0 & 0 & 1
+\end{pmatrix}
+\\
+R_x(\Theta)=
+\begin{pmatrix}
+    1 & 0 & 0 & 0 \\
+    0 & \cos\Theta & -\sin\Theta & 0 \\
+    0 & \sin\Theta & \cos\Theta & 0 \\
+    0 & 0 & 0 & 1
+\end{pmatrix}绕X轴旋转
+\\
+R_y(\Theta) =
+\begin{pmatrix}
+    \cos\Theta & 0 & \sin\Theta & 0 \\
+    0 & 1 & 0 & 0 \\
+    -\sin\Theta & 0 & \cos\Theta & 0 \\
+    0 & 0 & 0 & 1
+\end{pmatrix}绕Y轴旋转
+\\
+R_z(\Theta) = 
+\begin{pmatrix}
+    \cos\Theta & -\sin\Theta & 0 & 0 \\
+    \sin\Theta & \cos\Theta & 0 & 0 \\
+    0 & 0 & 1 & 0 \\
+    0 & 0 & 0 & 1
+\end{pmatrix}绕Z轴旋转
+\\
+R_{xyz}(\alpha, \beta, \sigma) = R_x(\alpha)R_y(\beta)R_z(\sigma)
 $$
 
-### 逆变换
+> 旋转时，绕哪个轴旋转，那个轴对应的坐标不变，所以x轴旋转的第一行第一列、y轴旋转的第二行第二列、z轴旋转的第三行第三列
 
-![逆变换](./Image/9.png)
+如何证明$R_{xyz}(\alpha, \beta, \sigma) = R_x(\alpha)R_y(\beta)R_z(\sigma)$成立，这个时候需要引入**罗德里格斯公式**
 
-逆变换就是把之前的操作反向来一次，对应的就是矩阵中的逆矩阵 
 
+### 视图变换 Camera/View
+
+视图就类似使用设计相机拍照，视图就是镜头中的世界  
+
+- 拍一张好照片需要
+  - 好的地方（Module），搭建场景
+  - 好的角度（view），视图变换
+  - 投影（三维空间投影到二维照片）
+
+综上，就是图形学渲染出效果的模型(Model)、视图(View)、投影(Projection)变换，简称MVP变换
+
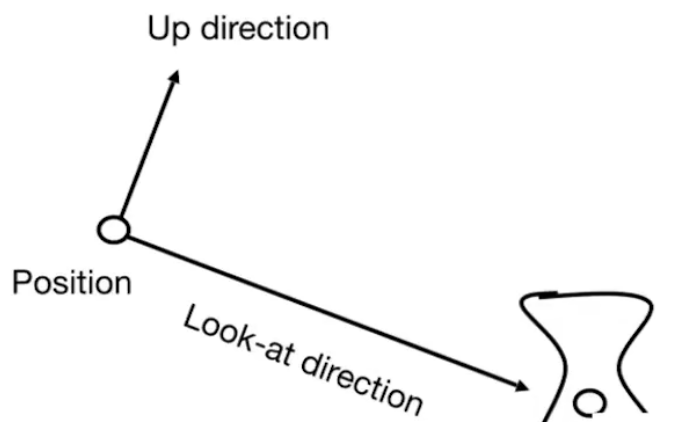
+- 定义相机
+  - 坐标
+  - 向上的向量(一个向量就可以确定相机的Roll)
+  - 朝向
+
+![](./Image/13.png)
+
+**约定：相机永远在原点，永远不动，永远以y轴向上，永远看向-Z轴**
+其他物体也跟着相机移动
+
+- 针对坐标为(x, y, z)，角度为(a, b, c)的相机，需要做哪些变换
+  1. 相机移动到原点坐标
+  2. 相机的朝向旋转到-Z轴方向
+  3. 相机的向上向量旋转到Y轴方向
+
+设定相机的朝向向量为g，相机向上的向量为t，可推得相机另一个轴的向量为$g \times t$
+
+$$
+T_{view} =
+\begin{bmatrix}
+    1 & 0 & 0 & -x_e \\
+    0 & 1 & 0 & -y_e \\
+    0 & 0 & 0 & -z_e
+\end{bmatrix} 坐标变换矩阵
+\\
+R^{-1}_{view} =
+\begin{bmatrix}
+    x_{g \times t} & x_t & x_{-g} & 0 \\
+    y_{g \times t} & y_t & y_{-g} & 0 \\
+    z_{g \times t} & z_t & z_{-g} & 0 \\
+    0 & 0 & 0 & 1
+\end{bmatrix} 不加证明给出矩阵R_{view}^{-1}
+\\
+R_{view}^{-1} * 
+\begin{bmatrix}
+    1 \\ 0 \\ 0
+\end{bmatrix} = 
+\begin{bmatrix}
+    x_{g \times t} \\
+    y_{g \times t} \\
+    z_{g \times t} \\
+\end{bmatrix} 可见R_{view}^{-1}乘以X轴、Y轴、Z轴都等于相机对应的向量坐标
+\\
+R^{-1}_{view} * 标准矩阵 = 相机矩阵 \Longrightarrow 相机矩阵 * R_{view} = 标准矩阵
+\\
+R_{view}^{-1}是R_{view}的逆矩阵
+\\
+R_{view} =
+\begin{bmatrix}
+    x_{g \times t} & y_{g \times t} &z_{g \times t} & 0 \\
+    x_t & y_t & z_t & 0 \\
+    x_{-g} & y_{-g} & z_{-g} & 0 \\
+    0 & 0 & 0 & 1
+\end{bmatrix} 不加证明给出矩阵R_{view}
+\\
+M_{view} = R_{view} T_{view} 组合后得出视图变换矩阵(从右往左的理解顺序，先平移、再旋转)
+$$
+
+相机和所有的物体都根据该模型移动到特定位置，此时相机肯定是在原点的、看向-Z轴，向上坐标为Y轴的，各个物体的相对位置不变  
+
+模型(单独对模型的操作)-视图(对相机的操作并同步到模型上)变换
+
+### 投影变换
+
+![](./Image/14.png)
+
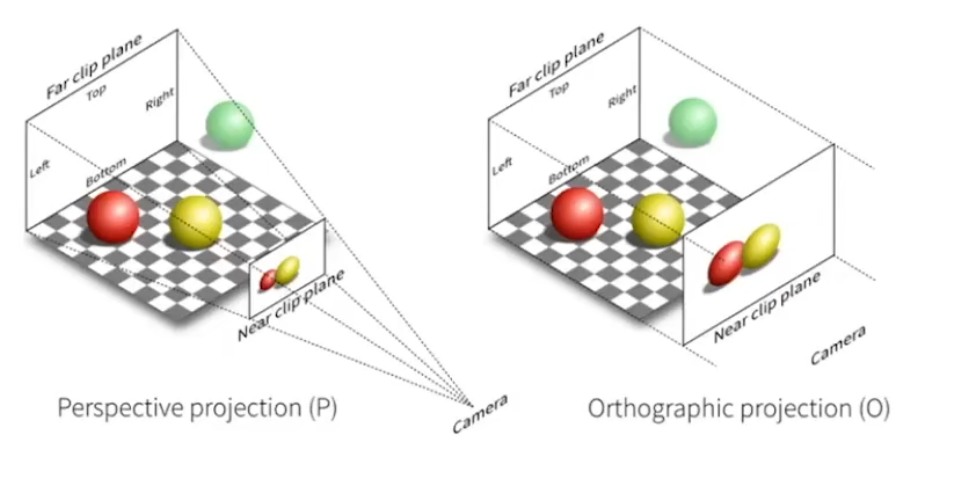
+> 图中左边为正交投影，右边是透视投影
+
+- 正交投影不会带来近大远小的世界效果，一般用于工程制图  
+- 透视投影会有近大远小
+
+![](./Image/15.png)
+
+> 图中左边为透视投影，右边为正交投影
+
+对于正交投影出来的图片结果，可以理解为相机在一个无限远的地方拍照，这样物体之间的距离差距就可以忽略不计了(走路月亮跟着你走的也是这个原因)
+
+#### 正交投影 Orthographic
+
+![](./Image/16.png)
+
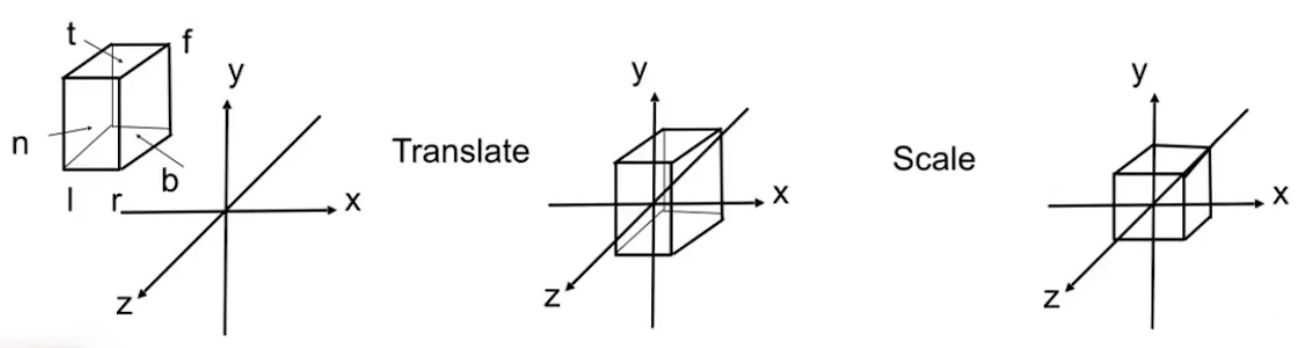
+- 在正交投影中定义一个矩阵，需要定义
+  - l(left)、r(right)，左平面距离矩形中心的距离和右平面距离矩形中心的距离
+  - t(top)、b(bottom)，上平面距离矩形中心的距离和下平面距离矩形中心的距离
+  - f(far)、r(near)，远平面距离矩形中心的距离和近平面距离矩形中心的距离
+
+> 因为相机朝向是-Z轴，所以f值一般小于r值
+
+在定义完一个矩形之后，需要将其通过一系列变换转换成图片中最右边的标准立方体(canonical cub $[-1 ,1]^3$)
+
+- 一系列变换指的是
+  - 矩形移动到原点
+  - X、Y、Z轴拉伸成\[-1, 1\]
+
+$$
+M_{ortho} =
+\begin{bmatrix}
+    \frac{2}{r-l} & 0 & 0 & 0 \\
+    0 & \frac{2}{t-b} & 0 & 0 \\
+    0 & 0 & \frac{2}{n-f} & 0 \\
+    0 & 0 & 0 & 1 
+\end{bmatrix} 
+\begin{bmatrix}
+    1 & 0 & 0 & -\frac{r+l}{2} \\
+    0 & 1 & 0 & -\frac{t+b}{2} \\
+    0 & 0 & 1 & -\frac{n+f}{2} \\
+    0 & 0 & 0 & 1
+\end{bmatrix}
+$$
+
+> 左边缩放矩阵、右边平移矩阵（操作顺序从右往左理解）  
+> 暂不考虑旋转
+
+这里对物体做了拉伸，未来还会做一次**视口变换**，**视口变换**时会再做一次拉伸
+
+#### 透视投影 Perspective
+
+理论上两条平行的先看起来相交了
+
+![](./Image/17.png)
+
+前置知识：点(x, y, z, 1)乘以k，得到(kx, ky, kz, k != 0)表示其实也是点(x, y, z, 1)，将k换成z，可以得到(xz, yz, $z^2$,z != 0)，也表示(x, y, z, 1)这个点  
+
+> (1, 0, 0, 1)与(2, 0, 0, 2)表示同一个点
+
+![](./Image/18.png)
+
+- 透视投影分两步 
+    1. 将Frustum平截头体转换成Cuboid矩形
+    2. 进行一次正交投影
+
+- 将Frustum平截头体转换成Cuboid矩形
+  - n(near)平面的四个点不会发生变换
+  - f(far)平面的z值不会发生变换，只是在平面内进行收缩
+  - n、f平面的中心点不会发生变化
+
+![](./Image/19.png)
+
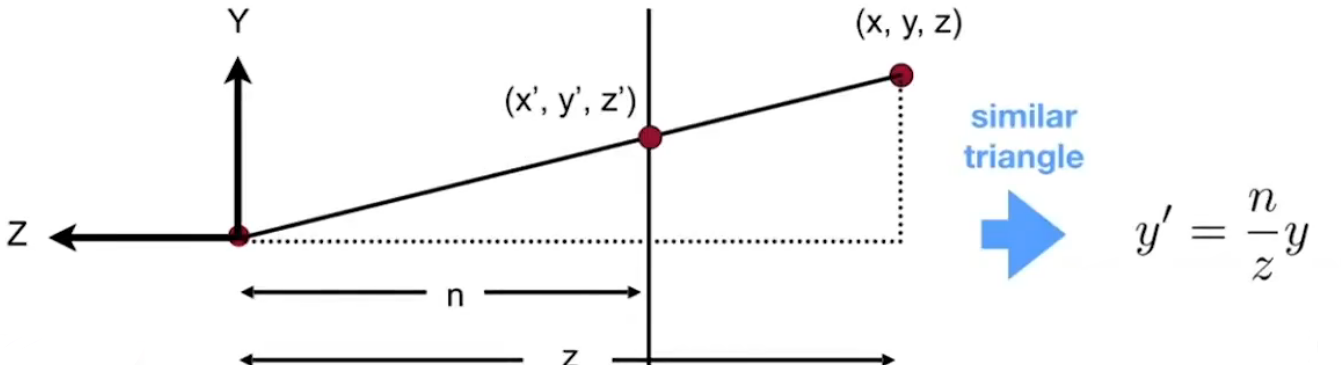
+通过侧面观察，更容易得到结论  
+
+最左边的红点就是摄像机的位置，中间的红点就是n(near)平面，最右边的红点就是f(far)平面  
+
+目标就是将(x, y, z) => (x, y\', z)，通过相似三角形可以推出计算公式
+
+设$M_{persp}$为透视变换矩阵
+
+设$M^{(4\times4)}_{persp \rightarrow ortho}$为透视变换成正交的变换矩阵
+
+得出$M_{persp}=M_{ortho}M^{(4\times4)}_{persp \rightarrow ortho}$，即将模型先变换成正交可以用的矩形，再通过正交变换矩阵计算
+
+$x`=\frac{n}{z}x,y`=\frac{n}{z}y$
+
+$$
+\begin{pmatrix}
+    x \\ y \\ z \\ 1
+\end{pmatrix}
+\Rightarrow
+\begin{pmatrix}
+    nx/x \\ ny/z \\ unknow \\ 1
+\end{pmatrix} ==
+\begin{pmatrix}
+    nx \\ ny \\ still unknow \\ z
+\end{pmatrix}
+\\
+M^{(4\times4)}_{persp \rightarrow ortho} 
+\begin{pmatrix}
+    x \\ y \\ z \\ 1
+\end{pmatrix} = 
+\begin{pmatrix}
+    nx \\ ny \\ unknow \\ z
+\end{pmatrix}
+\Rightarrow
+M^{(4\times4)}_{persp \rightarrow ortho} =
+\begin{pmatrix}
+    n & 0 & 0 & 0 \\
+    0 & n & 0 & 0 \\
+    ? & ? & ? & ? \\
+    0 & 0 & 1 & 0
+\end{pmatrix}
+$$
+
+> 透视变换矩阵最后一行完全可以是(0 0 0 z)，但是z是变量，到时候计算的时候还得实时带入z的真实值，对于计算机来说很麻烦，要开辟内存，还要传值，浪费资源
+
+- 此时带入观察到的两个细节
+  - 对近平面来说，(x, y, n, 1) (n表示近平面的z)与透视变换矩阵运算，其x、y、n值不变
+  - 对远平面来说，(x, y, f, 1) (f表示远平名的z)与透视变换矩阵运算，其f值不变
+  - 对远平面来说，(0, 0, f, 1) 与透视变换矩阵运算，其值不变，仍未(0, 0, f, 1)
+
+$$
+M^{(4\times4)}_{persp \rightarrow ortho} 
+\begin{pmatrix}
+    x \\ y \\ n \\ 1
+\end{pmatrix} = 
+\begin{pmatrix}
+    x \\ y \\ n \\ 1 
+\end{pmatrix} ==
+\begin{pmatrix}
+    nx \\ ny \\ n^2 \\ n 
+\end{pmatrix}
+\\
+设M^{(4\times4)}_{persp \rightarrow ortho}第三行为
+\begin{pmatrix}
+    A & B & C & D
+\end{pmatrix}
+带入上述式子的计算中得
+\begin{pmatrix}
+    A & B & C & D
+\end{pmatrix}
+\begin{pmatrix}
+    x \\ y \\ n \\ 1
+\end{pmatrix} = n^2
+\\
+得到A=0, B=0, C*n + B = n^2
+\\
+M^{(4\times4)}_{persp \rightarrow ortho} 
+\begin{pmatrix}
+    0 \\ 0 \\ f \\ 1
+\end{pmatrix} = 
+\begin{pmatrix}
+    0 \\ 0 \\ f \\ 1 
+\end{pmatrix} ==
+\begin{pmatrix}
+    0 \\ 0 \\ f^2 \\ f
+\end{pmatrix}
+\\
+带入前面推理(0, 0, C, D)式子中，得到 Cf + D = f^2
+\\
+\begin{matrix}
+    Cn + D = n^2 \\
+    Cf + D = f^2
+\end{matrix}
+\Longrightarrow
+\begin{matrix}
+    C = n + f \\
+    D = -nf
+\end{matrix}
+\\
+M^{(4\times4)}_{persp \rightarrow ortho} = 
+\begin{pmatrix}
+    n & 0 & 0 & 0 \\
+    0 & n & 0 & 0 \\
+    0 & 0 & n + f & -nf \\
+    0 & 0 & 1 & 0
+\end{pmatrix}
+$$
 
+将得到的矩阵与（x，y，z，1）相乘后z的值等于(-nf)*z^(-1)+(n+f),是个反比例函数，这个图像恒过（n，n）与（f，f），在n与f之间，z是下凹的，所以z变小了，即再f与n平面之间的点的z是会变小的
 
 # 光栅化